题目内容
19.图甲为验证牛顿第二定律的实验装置示意图.图中打点计时器的电源为50Hz的交流电源,打点的时间间隔用△t表示.在小车质量未知的情况下,某同学设计了一种方法用来探究“在外力一定的条件下,物体的加速度与其质量间的关系”.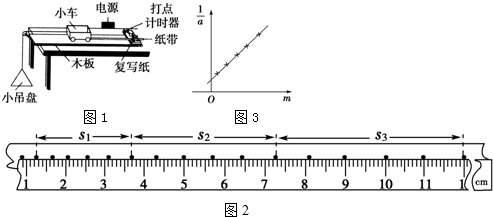
(1)本实验中,为了保证在改变小车中砝码的质量时小车所受的拉力近似不变,小吊盘和盘中物块的质量之和应满足的条件是远小于小车的质量.
(2)设纸带上三个相邻计数点的间距为s1、s2和s3.a可用s1、s3和△t表示为a=$\frac{{s}_{3}^{\;}-{s}_{1}^{\;}}{50△{t}_{\;}^{2}}$.图乙为用米尺测量某一纸带上的s1、s3的情况,由图可读出s1=24.2mm,s3=47.3mm,由此求得加速度的大小a=1.16m/s2.
(3)图丙为所得实验图线的示意图.设图中直线的斜率为k,在纵轴上的截距为b,若牛顿定律成立,则小车受到的拉力为$\frac{1}{k}$,小车的质量为$\frac{b}{k}$.
分析 为了保证在改变小车中砝码的质量时,小车所受的拉力近似不变,小吊盘和盘中物块的质量之和应该远小于小车和砝码的总质量.
根据连续相等时间内的位移之差是一恒量得出加速度.
由牛顿第二定律得出$\frac{1}{a}$-m的表达式,结合图线的斜率和截距进行求解.
解答 解:①设小车的质量为M,小吊盘和盘中物块的质量为m,设绳子上拉力为F,
以整体为研究对象有mg=(m+M)a
解得a=$\frac{mMg}{M+m}$,故有M>>m,即只有M>>m时才可以认为绳对小车的拉力大小等于小吊盘和盘中物块的重力.
②根据${s}_{3}^{\;}-{s}_{1}^{\;}=2a{T}_{\;}^{2}$得,T=5△t,则a=$\frac{{s}_{3}^{\;}-{s}_{1}^{\;}}{50△{t}_{\;}^{2}}$,由图可读出s1=24.2mm=0.0242m,s3=47.3mm=0.0473m,代入数据解得a=$\frac{0.0473-0.0242}{50×0.0{2}_{\;}^{2}}m/{s}_{\;}^{2}$=1.16m/s2.
③设小车质量为M,小车受到外力为F,由牛顿第二定律有F=(m+M)a;
所以$\frac{1}{a}=\frac{m}{F}+\frac{M}{F}$,则$\frac{1}{a}-m$图象的斜率为$\frac{1}{F}$,故F=$\frac{1}{k}$,纵轴截距为b=$\frac{M}{F}$,
则M=$\frac{b}{k}$.
故答案为:(1)远小于小车的质量 (2)$\frac{{s}_{3}^{\;}-{s}_{1}^{\;}}{50△{t}_{\;}^{2}}$ 24.2 47.3mm 1.16 (3)$\frac{1}{k}$ $\frac{b}{k}$
点评 实验问题要掌握实验原理、注意事项和误差来源;遇到涉及图象的问题时,要先根据物理规律写出关于纵轴与横轴的函数表达式,再根据斜率和截距的概念求解即可.

 如图所示,电路中A、B是两个完全相同的灯泡,L是一个自感系数很大、直流电阻为零的自感线圈,则下列判断正确的是( )
如图所示,电路中A、B是两个完全相同的灯泡,L是一个自感系数很大、直流电阻为零的自感线圈,则下列判断正确的是( )| A. | S刚闭合瞬间,A灯和B灯同时亮 | |
| B. | S闭合后电路稳定前,B先亮一下再逐渐变暗,A逐渐变暗 | |
| C. | S闭合电路稳定后,A灯和B灯亮度相同 | |
| D. | S闭合电路稳定后,再断开S时,A灯要亮一下再熄灭 |
 如图所示,物体在恒定拉力F的作用下沿水平面做匀速直线运动,运动速度为v,拉力F斜向上与水平面夹角为θ,则拉力F的功率可以表示为( )
如图所示,物体在恒定拉力F的作用下沿水平面做匀速直线运动,运动速度为v,拉力F斜向上与水平面夹角为θ,则拉力F的功率可以表示为( )| A. | Fv | B. | Fvcosθ | C. | Fvsinθ | D. | $\frac{Fv}{cosθ}$ |
| A. | 一直处于失重状态 | |
| B. | 一直处于超重状态 | |
| C. | 不受重力作用 | |
| D. | 处于失重还是超重状态由航天员工作状态决定 |
| A. | $\sqrt{\frac{2d}{a}}$ | B. | $\frac{2v}{a}$ | C. | $\frac{d}{v}$ | D. | $\frac{d}{2v}$ |
 一物体从一行星表面某高处自由下落(不计表层大气阻力).自开始下落计时,得到物体离该行星表面的高度h随时间t变化的图象如图所示,则( )
一物体从一行星表面某高处自由下落(不计表层大气阻力).自开始下落计时,得到物体离该行星表面的高度h随时间t变化的图象如图所示,则( )| A. | 行星表面重力加速度大小为8m/s2 | |
| B. | 行星表面重力加速度大小为10m/s2 | |
| C. | 物体落到行星表面时的速度大小为20m/s | |
| D. | 物体下落到行星表面的过程中平均速度大小为10m/s |



