题目内容
14．关于行星围绕太阳的运动，下列说法中正确的是（ ）| A． | 对于某一个行星，它距离太阳越近，运动速度越慢 | |
| B． | 对于某一个行星，它距离太阳越近，运动速度越快 | |
| C． | 距离太阳越远的行星，运动周期越短 | |
| D． | 行星的运转轨道都是圆形轨道 |
分析 根据开普勒关于行星运动的三定律解答．
解答 解：AB、根据在相等时间内，太阳和运动着的行星的连线所扫过的面积都是相等的，距离太阳越近线速度越大，故A错误，B正确；
C、根据开普勒第三定律：各个行星绕太阳公转周期的平方和它们的椭圆轨道的半长轴的立方成正比，知距离太阳越远的行星，运动周期越大，故C错误；
D、开普勒第一定律，也称椭圆定律：每一个行星都沿各自的椭圆轨道环绕太阳，而太阳则处在椭圆的一个焦点中．故D错误；
故选：B
点评 椭圆定律（开普勒第一定律） 开普勒第一定律，也称椭圆定律：每一个行星都沿各自的椭圆轨道环绕太阳，而太阳则处在椭圆的一个焦点中．面积定律（开普勒第二定律） 开普勒第二定律，也称面积定律：在相等时间内，太阳和运动着的行星的连线所扫过的面积都是相等的． 这一定律实际揭示了行星绕太阳公转的角动量守恒．调和定律（开普勒第三定律） 开普勒第三定律，也称调和定律：各个行星绕太阳公转周期的平方和它们的椭圆轨道的半长轴的立方成正比． 由这一定律不难导出：行星与太阳之间的引力与半径的平方成反比．这是牛顿的万有引力定律的一个重要基础．
练习册系列答案
相关题目
4．
如图所示，有两块金属板水平放置，两板间电势差为U．一个不计重力的带电粒子以初速度v0沿平行于两板的方向从正中间射入，穿过两板后又垂直于磁场方向进入边界线竖直的匀强磁场中．则粒子射入磁场和射出磁场的M、N两点间的距离d随着U和v0的变化情况为（ ）
如图所示，有两块金属板水平放置，两板间电势差为U．一个不计重力的带电粒子以初速度v0沿平行于两板的方向从正中间射入，穿过两板后又垂直于磁场方向进入边界线竖直的匀强磁场中．则粒子射入磁场和射出磁场的M、N两点间的距离d随着U和v0的变化情况为（ ）| A． | d随v0增大而增大，d与U无关 | B． | d随v0增大而增大，d随U增大而增大 | ||
| C． | d随U增大而增大，d与v0无关 | D． | d随v0增大而增大，d随U增大而减小 |
5．做直线运动的物体，在第1末、第2末、第3末的速度分别是1m/s，2m/s，3m/s，则物体的运动性质是（ ）
| A． | 一定是匀变速直线运动 | |
| B． | 一定是非匀变速直线运动 | |
| C． | 加速度不断增大的直线运动 | |
| D． | 可能是匀变速，也可能是非匀变速运动 |
2．
如图所示，在光滑水平面上有一个竖直向上的匀强磁场，分布在宽度为l的区域内．现有一个边长为a的正方形闭合导线框（a＜l），以初速度v0垂直于磁场边界沿水平面向右滑过该磁场区域，滑出时的速度为v．下列说法中正确的是（ ）
如图所示，在光滑水平面上有一个竖直向上的匀强磁场，分布在宽度为l的区域内．现有一个边长为a的正方形闭合导线框（a＜l），以初速度v0垂直于磁场边界沿水平面向右滑过该磁场区域，滑出时的速度为v．下列说法中正确的是（ ）| A． | 导线框完全进入磁场中时，速度大于$\frac{（{v}_{0}+v）}{2}$ | |
| B． | 导线框完全进入磁场中时，速度等于$\frac{（{v}_{0}+v）}{2}$ | |
| C． | 导线框完全进入磁场中时，速度小于$\frac{（{v}_{0}+v）}{2}$ | |
| D． | 以上三种都有可能 |
9．
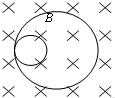一个静止的放射性原子核处于垂直纸面向里的匀强磁场中，由于发生了某种衰变而形成了如图所示的两个圆形径迹，两圆半径之比为1：16，有（ ）
一个静止的放射性原子核处于垂直纸面向里的匀强磁场中，由于发生了某种衰变而形成了如图所示的两个圆形径迹，两圆半径之比为1：16，有（ ）| A． | 该原子核发生了α衰变 | |
| B． | 该原子核发生了β衰变 | |
| C． | 那个打出衰变粒子的反冲核沿小圆作逆时针方向运动 | |
| D． | 该衰变过程结束后其系统的总质量略有增加 |
如图所示，质量为m、电荷量为+q的粒子从坐标原点O以初速度v0射出，粒子恰好经过A点，O、A两点长度为L，连线与坐标轴+y方向的夹角为α=37°，不计粒子的重力．（sin37°=0.6，cos37°=0.8）
3．
某人造地球卫星绕地球运行的椭圆轨道如图所示，E和F是椭圆轨道的两个焦点，卫星在A点的速度比在B点的速度大，则地球位于（ ）
某人造地球卫星绕地球运行的椭圆轨道如图所示，E和F是椭圆轨道的两个焦点，卫星在A点的速度比在B点的速度大，则地球位于（ ）| A． | F点 | B． | O点 | C． | E点 | D． | A点 |
4．
如图所示，A、B、C三个一样的滑块从粗糙固定斜面上的同一高度同时开始运动，A由静止释放，B的初速度方向沿斜面向下，大小为v0，C的初速度方向沿斜面水平，大小也为v0，下列说法中正确的是（ ）
如图所示，A、B、C三个一样的滑块从粗糙固定斜面上的同一高度同时开始运动，A由静止释放，B的初速度方向沿斜面向下，大小为v0，C的初速度方向沿斜面水平，大小也为v0，下列说法中正确的是（ ）| A． | 滑到斜面底端时，B的机械能减少最多 | |
| B． | 滑到斜面底端时，B的动能最大 | |
| C． | C的重力势能减少得多 | |
| D． | A、B、C三个物体到达底端的时间关系为：tB＜tC＜tA |