题目内容
14. 如图所示,两个倾角均为θ的光滑斜面固定在水平面上.甲、乙两个相同的小球(均视为质点)从斜面顶端同时以相同的速率v0分别向左水平抛出和沿斜面下滑,甲球不会落到斜面上,下列说法正确的是( )
如图所示,两个倾角均为θ的光滑斜面固定在水平面上.甲、乙两个相同的小球(均视为质点)从斜面顶端同时以相同的速率v0分别向左水平抛出和沿斜面下滑,甲球不会落到斜面上,下列说法正确的是( )| A. | 两球到达水平面时的动能相等 | |
| B. | 两球到达水平面时重力做功的功率相等 | |
| C. | 无论如何调节v0的值,乙球一定先到达水平面 | |
| D. | 若甲球恰好落至斜面底端,则甲球到达底端时的速度方向与水平方向的夹角为2θ |
分析 两球运动过程中,只有重力做功,机械能守恒,由机械能守恒定律分析到达水平面时动能的关系.根据P=mgvy,vy是竖直分速度,分析两球到达水平面时重力做功的功率的关系.根据运动学公式分析运动时间关系.由平抛运动的规律求甲球恰好落至斜面底端,速度方向与水平方向的夹角.
解答 解:A、设斜面的高度为h.根据机械能守恒定律得
mgh=Ek-$\frac{1}{2}m{v}_{0}^{2}$
则得,小球落到水平面时的动能 Ek=mgh+$\frac{1}{2}m{v}_{0}^{2}$,可知两球到达水平面时的动能相等.故A正确.
B、重力做功的功率P=mgvy,vy是竖直分速度,由于两球到达水平面时竖直分速度不一定相等,所以两球到达水平面时重力做功的功率不一定相等.故B错误.
C、对于甲球,落在水平面上与落在斜面底端的时间相等.甲球落在斜面上时,将其运动沿斜面方向和垂直于斜面方向分解,沿斜面的分初速度为v0cosθ,分加速度为gsinθ.甲球沿斜面方向做初速度为v0cosθ、加速度为gsinθ的匀加速运动.设斜面的长为L,则沿斜面方向有 L=v0cosθt甲+$\frac{1}{2}$gsinθ${t}_{甲}^{2}$.
对于乙球,加速度大小为 a=gsinθ,则有 L=v0t乙+$\frac{1}{2}$gsinθ${t}_{乙}^{2}$.
对比可得,t乙<t甲,可知,无论如何调节v0的值,乙球一定先到达水平面,故C正确.
D、设甲球到达底端时的速度方向与水平方向的夹角为α,则有
tanα=$\frac{{v}_{y}}{{v}_{0}}$
又tanθ=$\frac{y}{x}$=$\frac{\frac{{v}_{y}}{2}t}{{v}_{0}t}$=$\frac{{v}_{y}}{2{v}_{0}}$,则有 tanα=2tanθ,α≠2θ,故D错误.
故选:AC
点评 解决本题的关键知道平抛运动水平方向和竖直方向上的运动规律,结合牛顿第二定律和运动学公式综合分析.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案| A. | 卢瑟福通过α粒子散射实验证实了原子内部有一个体积很小的原子核 | |
| B. | 铀核(${\;}_{92}^{238}$U)衰变为铅核(${\;}_{82}^{206}$Pb)的过程中,要经过6次α衰变和8次β衰变 | |
| C. | 按照爱因斯坦的理论,在光电效应中,金属中的电子吸收一个光子获得的能量是hv,这些能量的一部分用来克服金属的逸出功W0,剩下的表现为逸出后电子的初动能Ek | |
| D. | 玻尔的原子理论第一次将量子观念引入原子领域,提出了定态和跃迁的概念,成功地解释了所有原子光谱的实验规律. | |
| E. | 铀核(${\;}_{92}^{238}$U)衰变成α粒子和另一原子核,衰变产物的结合能之和一定大于铀核的结合能 |
 某同学为研究电动机在启动和工作过程中电流的变化情况,设计如图所示的电路,则下列说法中正确的是( )
某同学为研究电动机在启动和工作过程中电流的变化情况,设计如图所示的电路,则下列说法中正确的是( )| A. | 电动机启动时的电流小于正常工作时的电流 | |
| B. | 电动机有负载时的电流小于空载时的电流 | |
| C. | 若增大电动机的负载,则电流增大 | |
| D. | 由于电动机内阻不变,因此电流与电动机的负载无关 |
 某研究性学习小组设计了如图甲所示的电路,同时测电阻R0的阻值、电源的电动势E及内阻r,
某研究性学习小组设计了如图甲所示的电路,同时测电阻R0的阻值、电源的电动势E及内阻r,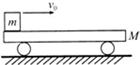 如图所示,质量为M=3kg的平板小车静止在光滑的水平面上,小车平板面离地面的高度h=1.8m,有一质量m=1kg的小物块(可视为质点)以v0=5m/s从小车左端滑上小车,在小车上运动2s后,从小车右端飞出,最后落在水平地面上,测得滑块滑上小车到落地过程中的水平位移大小为s=8.2m,重力加速度为g=10m/s2.求:
如图所示,质量为M=3kg的平板小车静止在光滑的水平面上,小车平板面离地面的高度h=1.8m,有一质量m=1kg的小物块(可视为质点)以v0=5m/s从小车左端滑上小车,在小车上运动2s后,从小车右端飞出,最后落在水平地面上,测得滑块滑上小车到落地过程中的水平位移大小为s=8.2m,重力加速度为g=10m/s2.求: 一棱镜的截面为直角三角形ABC,其中∠A=30°,在此截面所在的平面内,一条光线以i=45°的入射角从AC边的中点M射入棱镜,经过一次折射和全反射后垂直于BC边从E点射出,求:
一棱镜的截面为直角三角形ABC,其中∠A=30°,在此截面所在的平面内,一条光线以i=45°的入射角从AC边的中点M射入棱镜,经过一次折射和全反射后垂直于BC边从E点射出,求: 如题图所示,食盐(NaCl)晶体由钠离子和氯离子组成,相邻离子的中心用线连起来组成了一个个大小相等的立方体,立方体的个数与两种离子的总数目相等.已知食盐的密度为ρ,摩尔质量为M,阿伏加德罗常数为NA,求:
如题图所示,食盐(NaCl)晶体由钠离子和氯离子组成,相邻离子的中心用线连起来组成了一个个大小相等的立方体,立方体的个数与两种离子的总数目相等.已知食盐的密度为ρ,摩尔质量为M,阿伏加德罗常数为NA,求: