题目内容
20.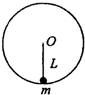 如图所示,长为L的轻杆一端固定一个质量为m的小球,另一端有光滑的固定轴O,现给球一初速度,使球和杆一起绕轴O在坚直平面内转动,不计空气阻力,则( )
如图所示,长为L的轻杆一端固定一个质量为m的小球,另一端有光滑的固定轴O,现给球一初速度,使球和杆一起绕轴O在坚直平面内转动,不计空气阻力,则( )| A. | 小球到达最高点的速度必须等于$\sqrt{GL}$ | |
| B. | 小球到达最高点的速度可能为0 | |
| C. | 小球到达最高点受杆的作用力一定为拉力 | |
| D. | 小球到达最高点受杆的作用力一定为支持力 |
分析 小球在竖直平面内做圆周运动,由指向圆心的合力提供向心力.在最高点,小球受到的弹力和重力的合力提供向心力,根据牛顿第二定律列式分析即可.
解答 解:AB、轻杆能支撑小球,所以小球到达最高点的最小速度为0,故A错误,B正确.
CD、设在最高点,轻杆对小球的作用力大小为F,方向向上,由牛顿第二定律得:
mg-F=m$\frac{{v}^{2}}{L}$…①
由①知,当v=$\sqrt{gL}$时,杆对球的作用力F=0;
当v>$\sqrt{gL}$,F<0,F向下,说明杆对球为拉力;当v<$\sqrt{gL}$,F>0,F向上,说明杆对球为支持力;故CD错误.
故选:B.
点评 本题关键对小球在最高点和最低点分别受力分析,然后根据牛顿第二定律列式分析,要注意,杆对小球可以无弹力,可以是拉力、支持力.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
11. 如图所示,用一根长为L质量不计的细杆与一个上弧长为l0、下弧长为d0的金属线框的中点联结并悬挂于O点,悬点正下方存在一个上弧长为2l0、下弧长为2d0的方向垂直纸面向里的匀强磁场,且d0<<L.先将线框拉开到如图所示位置,松手后让线框进入磁场,忽略空气阻力和摩擦.下列说法正确的是( )
如图所示,用一根长为L质量不计的细杆与一个上弧长为l0、下弧长为d0的金属线框的中点联结并悬挂于O点,悬点正下方存在一个上弧长为2l0、下弧长为2d0的方向垂直纸面向里的匀强磁场,且d0<<L.先将线框拉开到如图所示位置,松手后让线框进入磁场,忽略空气阻力和摩擦.下列说法正确的是( )
 如图所示,用一根长为L质量不计的细杆与一个上弧长为l0、下弧长为d0的金属线框的中点联结并悬挂于O点,悬点正下方存在一个上弧长为2l0、下弧长为2d0的方向垂直纸面向里的匀强磁场,且d0<<L.先将线框拉开到如图所示位置,松手后让线框进入磁场,忽略空气阻力和摩擦.下列说法正确的是( )
如图所示,用一根长为L质量不计的细杆与一个上弧长为l0、下弧长为d0的金属线框的中点联结并悬挂于O点,悬点正下方存在一个上弧长为2l0、下弧长为2d0的方向垂直纸面向里的匀强磁场,且d0<<L.先将线框拉开到如图所示位置,松手后让线框进入磁场,忽略空气阻力和摩擦.下列说法正确的是( )| A. | 金属线框最终将静止不动 | |
| B. | 金属线框dc边进入磁场与ab边离开磁场的速度大小相等 | |
| C. | 金属线框进入磁场时感应电流的方向为a→b→c→d→a | |
| D. | 金属线框离开磁场时感应电流的方向为a→b→c→d→a |
5.以下说法中正确的是( )
| A. | 牛顿发现了万有引力定律,被称为“称出地球质量的第一人” | |
| B. | 为了减小火车转弯时对铁轨的磨损,应当将内轨适当垫高一些 | |
| C. | 经典力学适用于宏观高速的物体,而不适用于微观低速的粒子 | |
| D. | 根据相对论可知,当物体高速运动时,质量将随速度的增大而增大 |
12. 如图所示,一气缸竖直倒放,气缸内有一质量不可忽略的活塞,将一定量的理想气体封在气缸内,活塞与气缸壁无摩擦,气体处于平衡状态.现保持温度不变,把气缸稍微倾一点,在达到平衡后,与原来相比,则( )
如图所示,一气缸竖直倒放,气缸内有一质量不可忽略的活塞,将一定量的理想气体封在气缸内,活塞与气缸壁无摩擦,气体处于平衡状态.现保持温度不变,把气缸稍微倾一点,在达到平衡后,与原来相比,则( )
 如图所示,一气缸竖直倒放,气缸内有一质量不可忽略的活塞,将一定量的理想气体封在气缸内,活塞与气缸壁无摩擦,气体处于平衡状态.现保持温度不变,把气缸稍微倾一点,在达到平衡后,与原来相比,则( )
如图所示,一气缸竖直倒放,气缸内有一质量不可忽略的活塞,将一定量的理想气体封在气缸内,活塞与气缸壁无摩擦,气体处于平衡状态.现保持温度不变,把气缸稍微倾一点,在达到平衡后,与原来相比,则( )| A. | 气体的压强变小 | B. | 气体的压强变大 | C. | 气体的体积变小 | D. | 气体的体积变大 |
9.下列说法正确的是( )
| A. | 倒影是因为光的反射形成的,色散是由于光的折射的缘故 | |
| B. | 水中的气泡看起来特别明亮,是因为光从水射向气泡时,一部分光在界面上发生了全反射 | |
| C. | 光的衍射否定光直线传播的结论 | |
| D. | 麦克斯韦提出电磁场理论并预言电磁波存在,后来由他又用实验证实电磁波的存在 |
 如图,在宽度分别为l1和l2的两个毗邻的条形区域分别有匀强磁场和匀强电场,磁场方向垂直于纸面向里,电场方向与电、磁分界线平行向右,一带正电荷的粒子以速率v从磁场区域上边界的P点斜射入磁场,然后以垂直于电、磁场分界线的交点到PQ的距离为d,不计重力,求电场强度与磁感应强度大小之比及粒子在磁场与电场中运动时间之比.
如图,在宽度分别为l1和l2的两个毗邻的条形区域分别有匀强磁场和匀强电场,磁场方向垂直于纸面向里,电场方向与电、磁分界线平行向右,一带正电荷的粒子以速率v从磁场区域上边界的P点斜射入磁场,然后以垂直于电、磁场分界线的交点到PQ的距离为d,不计重力,求电场强度与磁感应强度大小之比及粒子在磁场与电场中运动时间之比.
 如图甲所示,在xoy平面内存在半径为R=16cm的圆形有界磁场区域,有界磁场边界和x轴相切于O点,y轴上的P点为圆心,与y轴成60°角的MN为圆形有界场的一条直径,MN将磁场区域分成Ⅰ、Ⅱ两部分.x轴下方为随时间变化的电场,电场强度大小为E=8×10-3V/m,E-t图象如图乙所示,周期T=1.2×10-2s.当t=$\frac{T}{4}$时,第三象限的粒子源S沿y轴正方向发射比荷为108C/kg的粒子,粒子经坐标原点O由y轴左侧进入磁场区域Ⅰ,一次经P、M两点垂坠MN离开磁场.测得粒子在磁场中运动时间t=$\frac{π}{3}$×10-4s,重力不计.求:
如图甲所示,在xoy平面内存在半径为R=16cm的圆形有界磁场区域,有界磁场边界和x轴相切于O点,y轴上的P点为圆心,与y轴成60°角的MN为圆形有界场的一条直径,MN将磁场区域分成Ⅰ、Ⅱ两部分.x轴下方为随时间变化的电场,电场强度大小为E=8×10-3V/m,E-t图象如图乙所示,周期T=1.2×10-2s.当t=$\frac{T}{4}$时,第三象限的粒子源S沿y轴正方向发射比荷为108C/kg的粒子,粒子经坐标原点O由y轴左侧进入磁场区域Ⅰ,一次经P、M两点垂坠MN离开磁场.测得粒子在磁场中运动时间t=$\frac{π}{3}$×10-4s,重力不计.求: