题目内容
14.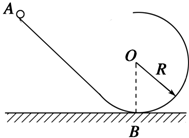 如图所示,光滑绝缘斜面的坡度为30°,其下端与半径为R的光滑绝缘半圆轨道平滑连接.现在使一带正电且质量为m的小球从斜面上的A点由静止释放,进入圆轨道后沿圆轨道运动.已知空间存在竖直向上的匀强电场,它对小球的电场力为其重力的一半.试求:
如图所示,光滑绝缘斜面的坡度为30°,其下端与半径为R的光滑绝缘半圆轨道平滑连接.现在使一带正电且质量为m的小球从斜面上的A点由静止释放,进入圆轨道后沿圆轨道运动.已知空间存在竖直向上的匀强电场,它对小球的电场力为其重力的一半.试求:(1)若小球能到达圆轨道的最高点,则释放点离地面的高度至少为多少?
(2)若小球释放点离地高度为4R,则此后小球对轨道的最大压力为多少?
(3)若小球从圆轨最高点飞出后恰能垂直地打在斜面上,则释放点离地面的高度应为多少?
分析 (1)小球刚好能到达圆轨道的最高点时,由重力和电场力的合力提供向心力,根据牛顿第二定律求得小球通过最高点的速度,再由动能定理即可求得释放点离地面的高度;
(2)小球能到达圆轨道的最低点时速度最大,小球对轨道的压力最大,由动能定理和牛顿第二定律结合解答.
(3)小球从圆轨最高点飞出后做类平抛运动,根据垂直地打在斜面上时速度方向,由运动的分解法求出小球通过圆轨最高点的速度,再由动能定理求释放点离地面的高度.
解答 解:(1)若小球能到达圆轨道的最高点,其速度v满足:
mg-qE=m$\frac{{v}^{2}}{R}$
又 qE=$\frac{1}{2}$mg
得:v=$\sqrt{\frac{1}{2}gR}$
从释放到过圆轨道最高点的过程,由动能定理得:
(mg-qE)(h-2R)=$\frac{1}{2}m{v}^{2}$-0
解得:h=2.5R
(2)小球能到达圆轨道的最低点时速度最大,小球对轨道的压力最大.从释放到最低点的过程,由动能定理得:
(mg-qE)H=$\frac{1}{2}m{v}_{1}^{2}$
在最低点,由牛顿第二定律得:
N-mg+qE=m$\frac{{v}_{1}^{2}}{R}$
联立解得:N=$\frac{9}{2}$mg
由牛顿第三定律得小球对轨道的最大压力为:N′=N=$\frac{9}{2}$mg
(3)设小球从圆轨最高点飞出后恰能垂直地打在斜面上时,通过圆轨道最高点的速度大小为v2.类平抛运动的时间为t,加速度为a.斜面的倾角为α.
根据牛顿第二定律得 mg-qE=ma,得:a=$\frac{1}{2}g$
由题意知,小球垂直地打在斜面上时速度与竖直方向的夹角为:θ=α=30°
则有 tanθ=$\frac{{v}_{2}}{at}$
水平方向有 x=v2t
竖直方向有 h′=$\frac{1}{2}a{t}^{2}$
由几何关系可得:tanα=$\frac{2R-h′}{x}$
联立解得 v2=$\sqrt{\frac{2}{5}gR}$
从释放到过圆轨道最高点的过程,由动能定理得:
(mg-qE)(H-2R)=$\frac{1}{2}m{v}_{2}^{2}$-0
解得 H=2.4R
答:(1)若小球能到达圆轨道的最高点,则释放点离地面的高度至少为2.5R.
(2)若小球释放点离地高度为4R,则此后小球对轨道的最大压力为$\frac{9}{2}$mg.
(3)若小球从圆轨最高点飞出后恰能垂直地打在斜面上,则释放点离地面的高度应为2.4R.
点评 本题是向心力、类平抛运动与动能定理等知识的综合,关键要抓住物块恰能通过最高点的临界条件,运用运动的分解法研究类平抛运动.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案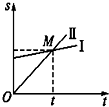 如图所示,Ⅰ、Ⅱ两条直线分别为描述P、Q两个物体的s-t图象.下列说法正确的是( )
如图所示,Ⅰ、Ⅱ两条直线分别为描述P、Q两个物体的s-t图象.下列说法正确的是( )| A. | M点表示两物体在t时刻相遇 | |
| B. | 两物体均做匀变速直线运动 | |
| C. | 在0-t时间内P的加速度较小 | |
| D. | 在0-t内,P比Q的速度大,在t以后P比Q的速度小 |
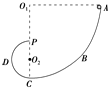 如图,竖直放置的粗糙四分之一圆弧轨道ABC与光滑半圆弧轨道CDP最低点重合在C点,圆心O1和O2在同一条竖直线上,圆弧ABC的半径为4R,半圆弧CDP的半径为R.一质量为m的小球从A点静止释放,到达P时与轨道间的作用力大小为mg,不计空气阻力.小球从A到P的过程中( )
如图,竖直放置的粗糙四分之一圆弧轨道ABC与光滑半圆弧轨道CDP最低点重合在C点,圆心O1和O2在同一条竖直线上,圆弧ABC的半径为4R,半圆弧CDP的半径为R.一质量为m的小球从A点静止释放,到达P时与轨道间的作用力大小为mg,不计空气阻力.小球从A到P的过程中( )| A. | 机械能减少了2mgR | B. | 克服摩擦力做功mgR | ||
| C. | 合外力做功mgR | D. | 重力势能减少了mgR |

| A. | 该电路图有错误,缺少一只与电流表相串联的保护电阻 | |
| B. | 用一节干电池做电源,稍旧电池比全新电池效果好 | |
| C. | 几节相串联的干电池比单独一节干电池做电源效果好 | |
| D. | 实验中滑动变阻器不能短路 |
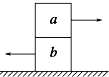 如图所示,质量均为m的两木块a与b叠放在水平地面上,a,b分别受到两个水平拉力的作用,两力大小均为F,两木块保持静止状态,则( )
如图所示,质量均为m的两木块a与b叠放在水平地面上,a,b分别受到两个水平拉力的作用,两力大小均为F,两木块保持静止状态,则( )| A. | a,b之间一定存在静摩擦力 | B. | b与地之间一定存在静摩擦力 | ||
| C. | b与地之间一定不存在静摩擦力 | D. | 地对b的支持力一定大于2mg |
| A. | 50N | B. | 350N | C. | 550N | D. | 850N |
| A. | 牵引力 | B. | 支持力 | C. | 重力 | D. | 摩擦力 |
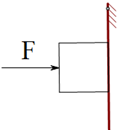 用200N水平方向的力把重50N的木块紧压在竖直墙上,如图所示,木块受到的摩擦力的大小是50N,方向是竖直向上,物块受到的支持力是200N.
用200N水平方向的力把重50N的木块紧压在竖直墙上,如图所示,木块受到的摩擦力的大小是50N,方向是竖直向上,物块受到的支持力是200N.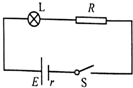 如图所示,电路中电阻R=10Ω,电源的内电阻r=2Ω,灯泡L上标有“3V,0.25A”的字样.闭合开关S,灯泡正常发光.求:
如图所示,电路中电阻R=10Ω,电源的内电阻r=2Ω,灯泡L上标有“3V,0.25A”的字样.闭合开关S,灯泡正常发光.求: