题目内容
17.如图甲所示,倾角θ为37°的传递带以恒定速度逆时针运行,现将一质量m=2kg的小物体轻轻放上传送带的A端,物体相对地面的速度随时间变化的关系如图乙,2s末物体到达B端,取沿传送带向下为正方向,g=10m/s2,sin37°=0.6,求:
(1)小物体在传送带A、B间的平均速度v;
(2)物体与传送带间的动摩擦因数μ;
(3)2s内物体机械能的变化量△E及因与传送带摩擦产生的内能Q.
分析 (1)物块轻放上传送带,开始所受的摩擦力沿斜面向下,当速度相等后,摩擦力沿传送带向上,从A到B做加速度不同的匀加速直线运动,根据速度时间图线与时间轴之间的面积求出位移,然后由:$\overline{v}=\frac{l}{t}$求出平均速度;
(2)求出0-1s内的加速度,从而得出合力的大小,求出速度相等后的加速度,结合牛顿第二定律求出动摩擦因数的大小.
(3)分别求出物体与传送带0-2s内的位移,由机械能的定义即可求出机械能的变化;求出相对运动的路程大小,最后求出摩擦产生的热量.
解答 解:(1)由v-t图象的面积规律可知传送带A、B间的距离L即为v-t图线与t轴所围的面积,所以:
$L=\frac{{v}_{1}}{t}•{t}_{1}+\frac{{v}_{1}+{v}_{2}}{2}{t}_{2}$,
代入数值得:L=16m
由平均速度的定义得:$v=\frac{L}{t}=\frac{16}{2}=8$m/s
(2)由v-t图象可知传送代运行速度为v1=10m/s,0-1s内物体的加速度为:${a}_{1}=\frac{△v}{△t}=\frac{10}{1}m/{s}^{2}=10m/{s}^{2}$,
则物体所受的合力为:F合=ma1=2×10N=20N.
1-2s内的加速度为:${a}_{2}=\frac{2}{1}=2m/{s}^{2}$,
根据牛顿第二定律得:${a}_{1}=\frac{mgsinθ+μmgcosθ}{m}$=gsinθ+μgcosθ,
${a}_{2}=\frac{mgsinθ-μmgcosθ}{m}$=gsinθ-μgcosθ
联立两式解得:μ=0.5,θ=37°.
(3)0-1s内,物块的位移:${x}_{1}=\frac{1}{2}{a}_{1}{{t}_{1}}^{2}=\frac{1}{2}×10×1m=5m$,
传送带的位移为:x2=vt1=10×1m=10m
则相对位移的大小为:△x1=x2-x1=5m,
则1-2s内,物块的位移为:${x}_{3}=v{t}_{2}+\frac{1}{2}{a}_{2}{{t}_{2}}^{2}$=$10×1+\frac{1}{2}×2×1m=11m$,
0-2s内物块向下的位移:L=x1+x3=5+11=16m
物块下降的高度:h=Lsin37°=16×0.6=9.6m
物块机械能的变化量:$△E=\frac{1}{2}m{v}_{B}^{2}-mgh$=$\frac{1}{2}×2×1{2}^{2}-2×10×9.6$=-48J
负号表示机械能减小.
1-2s内传送带的位移为:x4=vt2=10m,
则物块相对位移的大小为:△x2=x3-x4=1m,
所以相对路程的大小为:△s=△x1+△x2=6m,
摩擦产生的热量为:Q=μmgcosθ•△s=0.5×20×0.8×6J=48J.
答:(1)0~1s内物体所受的合外力大小为20N;
(2)小物块与传送带之间的动摩擦因数为0.5;
(3)在0~2s内物块的机械能减小48J,由于小物块与皮带间的摩擦所产生的热量为48J.
点评 该题考查传送带问题,解决本题的关键理清物块在传送带上的运动规律,结合牛顿第二定律、功能关系和运动学公式综合求解.


| A. | 卫星A的线速度较大 | B. | 卫星A的周期较大 | ||
| C. | 卫星A的角速度较大 | D. | 卫星A的加速度较大 |
 横截面为直角三角形的两个相同斜面紧靠在一起,固定在水平面上,如图所示.现有三个小球从左边斜面的顶点以不同的初速度向右平抛,最后落在斜面上.其落点分别是a、b、c.下列判断正确的是( )
横截面为直角三角形的两个相同斜面紧靠在一起,固定在水平面上,如图所示.现有三个小球从左边斜面的顶点以不同的初速度向右平抛,最后落在斜面上.其落点分别是a、b、c.下列判断正确的是( )| A. | 图中三小球比较,落在a点的小球飞行时间最短 | |
| B. | 图中三小球比较,落在c点的小球飞行时间最短 | |
| C. | 图中三小球比较,落在c点的小球飞行过程速度变化最小 | |
| D. | 图中三小球比较,落在a点的小球飞行过程速度变化最快 |
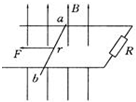 如图所示,固定在同一水平面内的两根平行长直金属导轨的间距为d,其右端接有阻值为R的电阻,整个装置处在竖直向上磁感应强度大小为B的匀强磁场中.一质量为m(质量分布均匀)的导体杆ab垂直于导轨放置,且与两导轨保持良好接触,杆与导轨之间的动摩擦因数为μ.现杆受到水平向左、垂直于杆的恒力F作用,从静止开始沿导轨运动,当运动距离L时,速度恰好达到最大(运动过程中杆始终与导轨保持垂直).设杆接入电路的电阻为r,导轨电阻不计,重力加速度大小为g.对于此过程,下列说法中正确的是( )
如图所示,固定在同一水平面内的两根平行长直金属导轨的间距为d,其右端接有阻值为R的电阻,整个装置处在竖直向上磁感应强度大小为B的匀强磁场中.一质量为m(质量分布均匀)的导体杆ab垂直于导轨放置,且与两导轨保持良好接触,杆与导轨之间的动摩擦因数为μ.现杆受到水平向左、垂直于杆的恒力F作用,从静止开始沿导轨运动,当运动距离L时,速度恰好达到最大(运动过程中杆始终与导轨保持垂直).设杆接入电路的电阻为r,导轨电阻不计,重力加速度大小为g.对于此过程,下列说法中正确的是( )| A. | 杆的速度最大值为$\frac{F(R+r)}{{B}^{2}{L}^{2}}$ | |
| B. | 当杆的速度达到最大时,a、b两端的电压为$\frac{F(R+r)}{BL}$ | |
| C. | 安倍力做功的绝对值等于回路中产生的焦耳热 | |
| D. | 恒力F做的功与安培力做的功之和等于杆动能的变化量 |
 “嫦娥二号”环月飞行的高度为100km,所探测到的有关月球的数据将比环月飞行高度为200km的“嫦娥一号”更加详实.若两颗卫星环月的运行均可视为匀速圆周运动,运行轨道如图所示.则( )
“嫦娥二号”环月飞行的高度为100km,所探测到的有关月球的数据将比环月飞行高度为200km的“嫦娥一号”更加详实.若两颗卫星环月的运行均可视为匀速圆周运动,运行轨道如图所示.则( )| A. | “嫦娥二号”环月运行的周期比“嫦娥一号”大 | |
| B. | “嫦娥二号”环月运行的线速度比“嫦娥一号”小 | |
| C. | “嫦娥二号”环月运行的向心力与“嫦娥一号”相等 | |
| D. | “嫦娥二号”环月运行的向心加速度比“嫦娥一号”大 |

 如图所示,长度l=0.50m的轻质细杆OA,A端固定一个质量m=3.0kg的小球,小球以O为圆心在竖直平面内做圆周运动.通过最高点时小球的速率是2.0m/s,g取10m/s2,试问:
如图所示,长度l=0.50m的轻质细杆OA,A端固定一个质量m=3.0kg的小球,小球以O为圆心在竖直平面内做圆周运动.通过最高点时小球的速率是2.0m/s,g取10m/s2,试问: