��Ŀ����
5��̫��ϵ�еĵڶ�������--���ǵ������ڶ࣬Ŀǰ�ѷ�����ʮ�ţ��±����й���������������������ǵ�һЩ����������������Ƚϣ������ж���ȷ���ǣ�������| ���� | �����ǵľ���/km | �뾶/km | ����/kg | ������ |
| ������ | 527 000 | 765 | 2.49��1021 | ������ |
| ������ | 1 222 000 | 2 575 | 1.35��1023 | �ݸ�˹ |
| A�� | ������Ĺ�ת���ڽ�С | B�� | ��������ת�����ٶȽϴ� | ||
| C�� | �����������ļ��ٶȽ�С | D�� | ������Ĺ�ת�ٶȽϴ� |
���� �ɿ����յ������ɷ�����ת���ڵĴ�С�������������ṩ���������Ƚ����ٶȵĴ�С�����ļ��ٶ��Լ����ٶȵĴ�С��
��� �⣺�����ǵ�����ΪM��
A���ɿ����յ�������$\frac{{R}^{3}}{{T}^{2}}=k$��֪���뾶Խ������Խ������������Ĺ�ת����С����A��ȷ��
B�������ǽ��ٶȹ�ʽ��=$\sqrt{\frac{GM}{{R}^{3}}}$��֪����ת�뾶RԽС�����ٶȦ�Խ����������Ĺ�ת���ٶȴ�B����
C�����������ļ��ٶȹ�ʽ$a=\frac{GM}{{R}^{2}}$��֪����ת�뾶RԽС�����ļ��ٶ�Խ���������������ļ��ٶȽ�С����C��ȷ��
D���������ٶȹ�ʽv=$\sqrt{\frac{GM}{R}}$��֪����ת�뾶RԽ�����ǵ����ٶ�ԽС����������Ĺ�ת�ٶȽϴ�D��ȷ��
��ѡ��ACD
���� �������������ͣ��ڽ�������ģ�͵Ļ����ϣ����������������ɺ�Բ���˶�֪ʶ����о����Ѷ����У�

��ϰ��ϵ�д�
�����Ŀ
15������Ӿ�ֹ��ʼ���ȼ���ֱ���˶�������ʱ�̿�ʼ������ͨ������λ��ʱ��ֱ�Ϊ1�롢2�롢3�룮����˵����ȷ���ǣ�������
| A�� | ����λ��֮��Ϊ1��8��27 | B�� | ����λ�Ƶ�ĩ�ٶ�֮��Ϊ1��2��3 | ||
| C�� | ����λ�Ƶ�ƽ���ٶ�֮��Ϊ1��8��27 | D�� | ����λ�Ƶ�ƽ���ٶ�֮��Ϊ1��3��5 |
13�������ʵ��������˶��������У���ȷ���ǣ�������
| A�� | �����˶�һ���DZ����˶� | |
| B�� | �����˶�һ���������˶� | |
| C�� | ��ƽ�����������£���������������˶� | |
| D�� | �ʵ��������˶�ʱ���ܵĺ����������ٶȷ�����ͬһֱ���� |
10��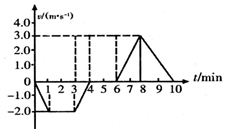 �ҹ��������š���DZ����7062m��ȴ�������DZ�����¼��Ԥʾ�ſ�������ȫ��99.8%�ĺ������磬��ij��ʵ��ʱ����DZ���ڵ���ʾ������ʾ���˴�ˮ�濪ʼ��DZ�����ˮ��10min��ȫ���̵��ٶ�-ʱ��ͼ����ͼ��֪��������
�ҹ��������š���DZ����7062m��ȴ�������DZ�����¼��Ԥʾ�ſ�������ȫ��99.8%�ĺ������磬��ij��ʵ��ʱ����DZ���ڵ���ʾ������ʾ���˴�ˮ�濪ʼ��DZ�����ˮ��10min��ȫ���̵��ٶ�-ʱ��ͼ����ͼ��֪��������
 �ҹ��������š���DZ����7062m��ȴ�������DZ�����¼��Ԥʾ�ſ�������ȫ��99.8%�ĺ������磬��ij��ʵ��ʱ����DZ���ڵ���ʾ������ʾ���˴�ˮ�濪ʼ��DZ�����ˮ��10min��ȫ���̵��ٶ�-ʱ��ͼ����ͼ��֪��������
�ҹ��������š���DZ����7062m��ȴ�������DZ�����¼��Ԥʾ�ſ�������ȫ��99.8%�ĺ������磬��ij��ʵ��ʱ����DZ���ڵ���ʾ������ʾ���˴�ˮ�濪ʼ��DZ�����ˮ��10min��ȫ���̵��ٶ�-ʱ��ͼ����ͼ��֪��������| A�� | ����ʵ����DZ������Ϊ6m | |
| B�� | ȫ�����������ٶȵĴ�С��2m/s2 | |
| C�� | �ӿ�ʼ������ͨ������·��Ϊ720m | |
| D�� | ��DZ�����뷵�ع��̵�ƽ���ٶ���ͬ |
17�� ��ͼ��ʾ���ڹ⻬��Եˮƽ���ϣ���������С��a��b��c�ֱ�λ�ڱ߳�ΪL���������ε����������ϣ�a��b�����磬�������Ϊ-q��c�����磮����ϵͳ����ˮƽ�������ǿ�糡�У���֪����������Ϊk��������С������ھ�ֹ״̬��������˵����ȷ���ǣ�������
��ͼ��ʾ���ڹ⻬��Եˮƽ���ϣ���������С��a��b��c�ֱ�λ�ڱ߳�ΪL���������ε����������ϣ�a��b�����磬�������Ϊ-q��c�����磮����ϵͳ����ˮƽ�������ǿ�糡�У���֪����������Ϊk��������С������ھ�ֹ״̬��������˵����ȷ���ǣ�������
 ��ͼ��ʾ���ڹ⻬��Եˮƽ���ϣ���������С��a��b��c�ֱ�λ�ڱ߳�ΪL���������ε����������ϣ�a��b�����磬�������Ϊ-q��c�����磮����ϵͳ����ˮƽ�������ǿ�糡�У���֪����������Ϊk��������С������ھ�ֹ״̬��������˵����ȷ���ǣ�������
��ͼ��ʾ���ڹ⻬��Եˮƽ���ϣ���������С��a��b��c�ֱ�λ�ڱ߳�ΪL���������ε����������ϣ�a��b�����磬�������Ϊ-q��c�����磮����ϵͳ����ˮƽ�������ǿ�糡�У���֪����������Ϊk��������С������ھ�ֹ״̬��������˵����ȷ���ǣ�������| A�� | ��ǿE�Ĵ�С����$\frac{2\sqrt{3}kq}{{L}^{2}}$�����������C�ĵ���� | |
| B�� | ��ǿE�Ĵ�С����$\frac{\sqrt{3}kq}{{L}^{2}}$�����������C�ĵ���� | |
| C�� | ��ǿE�Ĵ�С����$\frac{2\sqrt{3}kq}{{L}^{2}}$��������C�㴹ֱָ��ab���� | |
| D�� | ��ǿE�Ĵ�С����$\frac{\sqrt{3}kq}{{L}^{2}}$������ֱͨ��ab����ָ��C�� |


 ��ͼ��ʾ���ӵؽ�����A�İ뾶ΪR��������ɵĵ���ΪQ���������ĵľ���Ϊr����ý������ϸ�Ӧ���������O�������ij�ǿ��С����$\frac{kQ}{{r}^{2}}$��
��ͼ��ʾ���ӵؽ�����A�İ뾶ΪR��������ɵĵ���ΪQ���������ĵľ���Ϊr����ý������ϸ�Ӧ���������O�������ij�ǿ��С����$\frac{kQ}{{r}^{2}}$�� ��ͼ��ʾ��һ��ˮƽ��н�Ϊ��=37�����б����ƽ�е������㹻����һ���֣�ab��cd����֮�䣩���ڴ�ֱ����ƽ�����ϵ���ǿ�ų��У��ų��ĴŸ�Ӧǿ�ȴ�СΪB=2T���������L=1m���ײ�����һ��ֵΪR1=2���Ķ�ֵ���裬�ڴų��߽�cd�ڲ����������Ե������סһ����ΪM=2kg������䲿�ֵ���ΪR2=3���ĵ����MN����ʹһ����Ϊm=0.5kg������䲿�ֵ���Ϊr=0.3���ĵ����PQ�Ӵų��ϱ߽�ab�Ϸ��������ij�������»�������ų�ʱ���ٶ�v0=3m/s���������ʼ���뵼��Ӵ����ã��Ҵ�ֱ������ã�������費�ƣ�����һ��Ħ�����������ٶ�g=10m/s2��sin37��=0.6��cos37��=0.8��
��ͼ��ʾ��һ��ˮƽ��н�Ϊ��=37�����б����ƽ�е������㹻����һ���֣�ab��cd����֮�䣩���ڴ�ֱ����ƽ�����ϵ���ǿ�ų��У��ų��ĴŸ�Ӧǿ�ȴ�СΪB=2T���������L=1m���ײ�����һ��ֵΪR1=2���Ķ�ֵ���裬�ڴų��߽�cd�ڲ����������Ե������סһ����ΪM=2kg������䲿�ֵ���ΪR2=3���ĵ����MN����ʹһ����Ϊm=0.5kg������䲿�ֵ���Ϊr=0.3���ĵ����PQ�Ӵų��ϱ߽�ab�Ϸ��������ij�������»�������ų�ʱ���ٶ�v0=3m/s���������ʼ���뵼��Ӵ����ã��Ҵ�ֱ������ã�������費�ƣ�����һ��Ħ�����������ٶ�g=10m/s2��sin37��=0.6��cos37��=0.8��