题目内容
12.写出需要向心力的4个表达式:Fn=$m\frac{{v}^{2}}{r}$;Fn=mrω2;Fn=mvω;Fn=$mr\frac{4{π}^{2}}{{T}^{2}}$.分析 解答本题的关键是熟练掌握向心加速度的各种表达式,从而进一步写出向心力的表达式.
解答 解:我们知道向心加速度的表达式有:a=$\frac{{v}^{2}}{r}=r{ω}^{2}=vω=r\frac{4{π}^{2}}{{T}^{2}}$
根据F+ma知,向心力表达式为:Fn=$m\frac{{v}^{2}}{r}$=mrω2=mvω=$mr\frac{4{π}^{2}}{{T}^{2}}$.
故答案为:Fn=$m\frac{{v}^{2}}{r}$,Fn=mrω2,Fn=mvω,Fn=$mr\frac{4{π}^{2}}{{T}^{2}}$.
点评 本题属于简单基础题目,要明确各种向心力的表达式,并能在具体问题中进行正确应用.

练习册系列答案
相关题目
8. 如图所示,斜面与水平面、斜面与挡板间的夹角均为30°,一小球放置在斜面与挡板之间,挡板对小球的弹力为FN1,斜面对小球的弹力为FN2,以挡板与斜面连接点所形成的水平直线为轴,将挡板从图示位置开始缓慢地转到水平位置,不计摩擦,在此过程中( )
如图所示,斜面与水平面、斜面与挡板间的夹角均为30°,一小球放置在斜面与挡板之间,挡板对小球的弹力为FN1,斜面对小球的弹力为FN2,以挡板与斜面连接点所形成的水平直线为轴,将挡板从图示位置开始缓慢地转到水平位置,不计摩擦,在此过程中( )
 如图所示,斜面与水平面、斜面与挡板间的夹角均为30°,一小球放置在斜面与挡板之间,挡板对小球的弹力为FN1,斜面对小球的弹力为FN2,以挡板与斜面连接点所形成的水平直线为轴,将挡板从图示位置开始缓慢地转到水平位置,不计摩擦,在此过程中( )
如图所示,斜面与水平面、斜面与挡板间的夹角均为30°,一小球放置在斜面与挡板之间,挡板对小球的弹力为FN1,斜面对小球的弹力为FN2,以挡板与斜面连接点所形成的水平直线为轴,将挡板从图示位置开始缓慢地转到水平位置,不计摩擦,在此过程中( )| A. | FN1始终减小,FN2始终增大 | B. | FN1始终增大,FN2始终减小 | ||
| C. | FN1始终减小,FN2先减小后增大 | D. | FN1先减小后增大,FN2始终减小 |
7.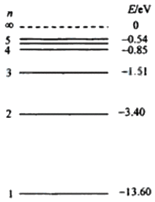 如图所示,为氢原子能级图,现有大量氢原子从n=4的能级发生跃迁,并发射光子照射一个钠光管,其逸出功为2.29ev,以下说法正确的是( )
如图所示,为氢原子能级图,现有大量氢原子从n=4的能级发生跃迁,并发射光子照射一个钠光管,其逸出功为2.29ev,以下说法正确的是( )
 如图所示,为氢原子能级图,现有大量氢原子从n=4的能级发生跃迁,并发射光子照射一个钠光管,其逸出功为2.29ev,以下说法正确的是( )
如图所示,为氢原子能级图,现有大量氢原子从n=4的能级发生跃迁,并发射光子照射一个钠光管,其逸出功为2.29ev,以下说法正确的是( )| A. | 氢原子能发出6种不同频率的光 | |
| B. | 能够让钠光电管发生光电效应现象的有3种光子 | |
| C. | 光电管发出的光电子与原子核发生β衰变时飞出的电子都是来源于原子核内部 | |
| D. | 钠光电管发出的光电子最多能够让氢原子从n=1的能级跃n=2的能级 |
17. 铁路在弯道处的内外轨道高度是不同的,已知内外轨道平面与水平面的夹角为θ,如图所示,弯道处的圆弧半径为R,若质量为m的火车转弯时速度等于$\sqrt{gRtanθ}$,则( )
铁路在弯道处的内外轨道高度是不同的,已知内外轨道平面与水平面的夹角为θ,如图所示,弯道处的圆弧半径为R,若质量为m的火车转弯时速度等于$\sqrt{gRtanθ}$,则( )
 铁路在弯道处的内外轨道高度是不同的,已知内外轨道平面与水平面的夹角为θ,如图所示,弯道处的圆弧半径为R,若质量为m的火车转弯时速度等于$\sqrt{gRtanθ}$,则( )
铁路在弯道处的内外轨道高度是不同的,已知内外轨道平面与水平面的夹角为θ,如图所示,弯道处的圆弧半径为R,若质量为m的火车转弯时速度等于$\sqrt{gRtanθ}$,则( )| A. | 火车轮缘对内外轨道无挤压 | |
| B. | 内轨对内侧车轮轮缘有挤压 | |
| C. | 这时铁轨对火车的支持力等于$\frac{mg}{cosθ}$ | |
| D. | 这时铁轨对火车的支持力大于$\frac{mg}{cosθ}$ |
1.在铁路转弯处,往往使外轨略高于内轨,关于这点下列说法不正确的是( )
| A. | 减轻火车轮子对外轨的挤压 | |
| B. | 减轻火车轮子对内轨的挤压 | |
| C. | 使火车车身倾斜,利用重力和支持力的合力提供转弯所需向心力 | |
| D. | 限制火车向外脱轨 |
2.“嫦娥三号”是我国第一个月球软着陆无人探测器.当它在距月球表面为100km的圆形轨道上运行时,周期为118min.已知月球半径和引力常量,由此可推算出( )
| A. | 月球的质量 | B. | “嫦娥三号”的质量 | ||
| C. | 月球的第一宇宙速度 | D. | “嫦娥三号”在该轨道上的运行速度 |
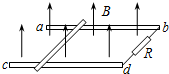 如图所示,在同一水平面的两金属导轨ab、cd相互平行,相距为d,一根质量为m的金属棒放在导轨上,与导轨垂直,在两导轨的b、d两端用与导轨垂直的导线,连接一阻值为R的电阻,其于电阻不计,导线与金属棒的间距为d,棒与导轨间的滑动摩擦因数为μ,最大静摩擦力等于滑动摩擦力,重力加速度为g.现在上述装置所在的区域加一竖直向上的匀强磁场,开始时,匀强磁场的磁感应强度大小为0,从t=0时刻起,磁感应强度均匀增加,且磁感应强度的变化率$\frac{△B}{△t}$=k,求:
如图所示,在同一水平面的两金属导轨ab、cd相互平行,相距为d,一根质量为m的金属棒放在导轨上,与导轨垂直,在两导轨的b、d两端用与导轨垂直的导线,连接一阻值为R的电阻,其于电阻不计,导线与金属棒的间距为d,棒与导轨间的滑动摩擦因数为μ,最大静摩擦力等于滑动摩擦力,重力加速度为g.现在上述装置所在的区域加一竖直向上的匀强磁场,开始时,匀强磁场的磁感应强度大小为0,从t=0时刻起,磁感应强度均匀增加,且磁感应强度的变化率$\frac{△B}{△t}$=k,求: 如图所示,MN是水平轨道,NP是倾角θ=45°的无限长斜轨道,长为L=0.8m的细线一端固定在O点,另一端系着质量为mB=2kg小球B,当细线伸直时B球刚好与MN轨道接触但没有挤压.开始时细线伸直,B球静止在MN轨道上,在MN轨道上另一个质量为mA=3kg小球A以速度v0向右运动.(不计一切摩擦及空气阻力,重力加速度g=10m/s2)
如图所示,MN是水平轨道,NP是倾角θ=45°的无限长斜轨道,长为L=0.8m的细线一端固定在O点,另一端系着质量为mB=2kg小球B,当细线伸直时B球刚好与MN轨道接触但没有挤压.开始时细线伸直,B球静止在MN轨道上,在MN轨道上另一个质量为mA=3kg小球A以速度v0向右运动.(不计一切摩擦及空气阻力,重力加速度g=10m/s2)