题目内容
9. 如图所示,在固定倾斜光滑杆上套有一个质量为m的圆环,杆与水平方向的夹角α=30°,圆环与竖直放置的轻质弹簧上端相连,弹簧的另一端固定在地面上的A点,弹簧处于原长h.让圆环沿杆由静止滑下,滑到杆的底端时速度恰为零.则在圆环下滑过程中( )
如图所示,在固定倾斜光滑杆上套有一个质量为m的圆环,杆与水平方向的夹角α=30°,圆环与竖直放置的轻质弹簧上端相连,弹簧的另一端固定在地面上的A点,弹簧处于原长h.让圆环沿杆由静止滑下,滑到杆的底端时速度恰为零.则在圆环下滑过程中( )| A. | 圆环和地球组成的系统机械能守恒 | |
| B. | 弹簧的最大弹性势能为mgh | |
| C. | 当弹簧垂直于光滑杆时圆环的动能最大 | |
| D. | 弹簧转过60°角时,圆环的动能为$\frac{mgh}{2}$ |
分析 分析圆环沿杆下滑的过程的受力和做功情况,只有重力弹簧的拉力做功,所以圆环机械能不守恒,但是系统的机械能守恒;沿杆方向合力为零的时刻,圆环的速度最大;当圆环的速度变为零时,弹簧的形变量最大,此时弹性势能最大;根据动能定理可以求出弹簧转过60°角时,圆环的动能的大小.
解答 解:A、圆环沿杆滑下,滑到杆底端的过程中有两个力对圆环做功,即环的重力和弹簧的拉力,所以圆环和地球组成的系统机械能不守恒,如果把圆环和弹簧组成的系统作为研究对象,则系统的机械能守恒,故A错误;
B、根据功能关系可知,当圆环滑到最底端时其速度为零,重力势能全部转化为弹性势能,此时弹性势能最大,等于重力势能的减小量,即为mgh,故B正确;
C、当弹簧垂直于光滑杆时,圆环的合力沿杆向下,圆环仍在加速,所以此时圆环的动能不是最大.当圆环沿杆的加速度为零时,其速度最大,动能最大,此时弹簧处于伸长状态,故C错误;
D、弹簧转过60°角时,此时弹簧仍为原长,以圆环为研究对象,利用动能定理得:mg•$\frac{h}{2}$=$\frac{1}{2}$mv2,即圆环的动能等于$\frac{mgh}{2}$,故D正确.
故选:BD
点评 对物理过程进行受力情况、运动情况、做功情况分析,是解决问题的根本方法.要注意对于圆环来说机械能并不守恒,但对圆环和弹簧组成的系统作为研究对象,系统的机械能是守恒的.

练习册系列答案
相关题目
19. 如图所示,L1和L2是不计电阻的输电线,甲是电压互感器,乙是电流互感器.若已知甲的变压比为500:1,乙的变流比为200:1,并且已知加在电压表两端的电压为220V,通过电流表的电流为5A,则输电线的输送功率为( )
如图所示,L1和L2是不计电阻的输电线,甲是电压互感器,乙是电流互感器.若已知甲的变压比为500:1,乙的变流比为200:1,并且已知加在电压表两端的电压为220V,通过电流表的电流为5A,则输电线的输送功率为( )
 如图所示,L1和L2是不计电阻的输电线,甲是电压互感器,乙是电流互感器.若已知甲的变压比为500:1,乙的变流比为200:1,并且已知加在电压表两端的电压为220V,通过电流表的电流为5A,则输电线的输送功率为( )
如图所示,L1和L2是不计电阻的输电线,甲是电压互感器,乙是电流互感器.若已知甲的变压比为500:1,乙的变流比为200:1,并且已知加在电压表两端的电压为220V,通过电流表的电流为5A,则输电线的输送功率为( )| A. | 1.1×108W | B. | 1.1×106W | C. | 1.1×l04W | D. | 1.1×102W |
20. 理想变压器初级线圈接一稳定的交变电流,电路连接如图所示,分别按下列方式操作,下列说法正确的是( )
理想变压器初级线圈接一稳定的交变电流,电路连接如图所示,分别按下列方式操作,下列说法正确的是( )
 理想变压器初级线圈接一稳定的交变电流,电路连接如图所示,分别按下列方式操作,下列说法正确的是( )
理想变压器初级线圈接一稳定的交变电流,电路连接如图所示,分别按下列方式操作,下列说法正确的是( )| A. | 只将S2从4拨向3,电流表示数变小 | |
| B. | 只将S3从闭合变为断开,电阻R2两端电压增大 | |
| C. | 只将变阻器S3的滑动触头上移,变压器的输入功率减小 | |
| D. | 只将S1从1拨向2,电流表示数变小 |
4.一理想变压器与电阻R、交流电压表V、电流表A按图甲所示方式连接,R=10Ω,变压器的匝数比为$\frac{{n}_{1}}{{n}_{2}}$=$\frac{10}{1}$.图乙是R两端电压U随时间变化的图象,Um=10$\sqrt{2}$V.下列说法中正确的是( )


| A. | 通过R的电流iR=$\sqrt{2}$cos50πtA | B. | 电流表A的读数为0.1A | ||
| C. | 电流表A的读数为$\frac{\sqrt{2}}{10}$A | D. | 电压表V的读数为10$\sqrt{2}$V |
19.如图所示,直线甲、乙分别表示两个做直线运动物体的v-t图象,下列说法正确的是( )
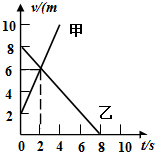

| A. | 甲沿正向做匀加速直线运动,乙沿反向做匀减速直线运动 | |
| B. | 甲比乙速度变化得快 | |
| C. | 2秒末甲乙相遇 | |
| D. | 2秒末甲乙速度相同 |

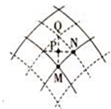 如图所示,某时刻两列频率相同、振幅为A的横波在叠加区域相遇,其中虚线表示波谷,实线表示波峰,相邻虚实线之间间隔距离为a,从虚线传播到相邻实线的时间为t,P点为QM的中点,其中M、N两点中振动始终加强的是M点,两列波的频率为$\frac{1}{2t}$,从图示时刻开始经2.5t的时间,P点的位移大小为2A.
如图所示,某时刻两列频率相同、振幅为A的横波在叠加区域相遇,其中虚线表示波谷,实线表示波峰,相邻虚实线之间间隔距离为a,从虚线传播到相邻实线的时间为t,P点为QM的中点,其中M、N两点中振动始终加强的是M点,两列波的频率为$\frac{1}{2t}$,从图示时刻开始经2.5t的时间,P点的位移大小为2A.