题目内容
1. 如图所示,滑块A、B的质量分别为2m和m,由轻质弹簧相连,置于光滑水平面上,把两滑块拉至近,使弹簧处于压缩状态后用一轻绳绑紧,两滑块一起以恒定的速率V0向右滑动.若突然断开轻绳,当弹簧第一次恢复原长时,滑块A的动能变为原来的4倍.求弹簧第一次恢复到原长时B的速度和最初弹性势能.
如图所示,滑块A、B的质量分别为2m和m,由轻质弹簧相连,置于光滑水平面上,把两滑块拉至近,使弹簧处于压缩状态后用一轻绳绑紧,两滑块一起以恒定的速率V0向右滑动.若突然断开轻绳,当弹簧第一次恢复原长时,滑块A的动能变为原来的4倍.求弹簧第一次恢复到原长时B的速度和最初弹性势能.
分析 根据滑块A动能的变化得出A的速度大小和方向,结合动量守恒定律求出弹簧第一次恢复原长时B的速度,根据能量守恒求出最初的弹性势能.
解答 解:因为当弹簧第一次恢复原长时,滑块A的动能变为原来的4倍,可知第一次恢复原长时A的速度大小为2v0,方向向左,设B的速度为v,规定向右为正方向,根据动量守恒得:3mv0=mv-2m•2v0,
解得:v=7v0.
根据机械能守恒得,最初的弹性势能为:
${E}_{p}=\frac{1}{2}•2m(2{v}_{0})^{2}+\frac{1}{2}m{v}^{2}-\frac{1}{2}•3m{{v}_{0}}^{2}$=$27m{{v}_{0}}^{2}$.
答:弹簧第一次恢复原长时B的速度为7v0,最初弹性势能为$27m{{v}_{0}}^{2}$.
点评 本题考查了动量守恒和能量守恒的基本运用,知道A、B和弹簧组成的系统动量守恒,根据动能的变化得出A的速度大小和方向是解决本题的关键.

练习册系列答案
相关题目
12. 如图所示,质量为m的小物块A(可视为质点)放在质量为M、长度为L的木板B右端,B置于光滑水平地面,系统处于静止状态,现对B施加一水平向右的恒定拉力F,A恰好不从B的左端掉下,A与B间的动摩擦因数为μ.则在此过程中( )
如图所示,质量为m的小物块A(可视为质点)放在质量为M、长度为L的木板B右端,B置于光滑水平地面,系统处于静止状态,现对B施加一水平向右的恒定拉力F,A恰好不从B的左端掉下,A与B间的动摩擦因数为μ.则在此过程中( )
 如图所示,质量为m的小物块A(可视为质点)放在质量为M、长度为L的木板B右端,B置于光滑水平地面,系统处于静止状态,现对B施加一水平向右的恒定拉力F,A恰好不从B的左端掉下,A与B间的动摩擦因数为μ.则在此过程中( )
如图所示,质量为m的小物块A(可视为质点)放在质量为M、长度为L的木板B右端,B置于光滑水平地面,系统处于静止状态,现对B施加一水平向右的恒定拉力F,A恰好不从B的左端掉下,A与B间的动摩擦因数为μ.则在此过程中( )| A. | 物块B克服摩擦力做的功为μmgL. | |
| B. | 系统因摩擦产生的热量为μmgL. | |
| C. | B克服摩擦力做的功大于摩擦力对A做的功. | |
| D. | 力F对B做的功等于B的动能的增加量与B克服摩擦力做的功之和. |
16.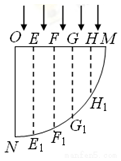 如图是一个$\frac{1}{4}$圆柱体棱镜的截面图,图中E、F、G、H将半径OM分成5等份,虚线EE1、FF1、GG1、HH1平行于半径ON,ON边可吸收到达其上的所有光线.已知该棱镜的折射率n=$\frac{5}{2}$,若平行光束垂直入射并覆盖OM,则光线( )
如图是一个$\frac{1}{4}$圆柱体棱镜的截面图,图中E、F、G、H将半径OM分成5等份,虚线EE1、FF1、GG1、HH1平行于半径ON,ON边可吸收到达其上的所有光线.已知该棱镜的折射率n=$\frac{5}{2}$,若平行光束垂直入射并覆盖OM,则光线( )
 如图是一个$\frac{1}{4}$圆柱体棱镜的截面图,图中E、F、G、H将半径OM分成5等份,虚线EE1、FF1、GG1、HH1平行于半径ON,ON边可吸收到达其上的所有光线.已知该棱镜的折射率n=$\frac{5}{2}$,若平行光束垂直入射并覆盖OM,则光线( )
如图是一个$\frac{1}{4}$圆柱体棱镜的截面图,图中E、F、G、H将半径OM分成5等份,虚线EE1、FF1、GG1、HH1平行于半径ON,ON边可吸收到达其上的所有光线.已知该棱镜的折射率n=$\frac{5}{2}$,若平行光束垂直入射并覆盖OM,则光线( )| A. | 只能从圆孤NF1射出 | B. | 只能从圆孤NG1射出 | ||
| C. | 可能从圆孤G1H1射出 | D. | 可能从圆孤H1M射出 |
13.下列描述中的计时数据表示时间间隔的是( )
| A. | 发射的子弹经0.5s击中目标 | |
| B. | 火车到站时间为17点30分 | |
| C. | 中央电视台新闻联播首播时间为19点整 | |
| D. | 2014年12月20日8点30分物理学科学业水平考试开考 |
10. 2017年5月23日,第八届中国卫星导航学术年会在上海召开,本届年会以“定位,万物互联”为主题.据悉中国将于2017年下半年开始发射北斗三号卫星.北斗导航卫星的发射需要经过几次变轨,例如某次变轨,先将卫星发射至近地圆轨道1上,然后在P处变轨到椭圆轨道2上,最后由轨道2在Q处变轨进入圆轨道3,轨道1、2相切于P点,轨道2、3相切于Q点.忽略空气阻力和卫星质量的变化,则以下说法正确的是( )
2017年5月23日,第八届中国卫星导航学术年会在上海召开,本届年会以“定位,万物互联”为主题.据悉中国将于2017年下半年开始发射北斗三号卫星.北斗导航卫星的发射需要经过几次变轨,例如某次变轨,先将卫星发射至近地圆轨道1上,然后在P处变轨到椭圆轨道2上,最后由轨道2在Q处变轨进入圆轨道3,轨道1、2相切于P点,轨道2、3相切于Q点.忽略空气阻力和卫星质量的变化,则以下说法正确的是( )
 2017年5月23日,第八届中国卫星导航学术年会在上海召开,本届年会以“定位,万物互联”为主题.据悉中国将于2017年下半年开始发射北斗三号卫星.北斗导航卫星的发射需要经过几次变轨,例如某次变轨,先将卫星发射至近地圆轨道1上,然后在P处变轨到椭圆轨道2上,最后由轨道2在Q处变轨进入圆轨道3,轨道1、2相切于P点,轨道2、3相切于Q点.忽略空气阻力和卫星质量的变化,则以下说法正确的是( )
2017年5月23日,第八届中国卫星导航学术年会在上海召开,本届年会以“定位,万物互联”为主题.据悉中国将于2017年下半年开始发射北斗三号卫星.北斗导航卫星的发射需要经过几次变轨,例如某次变轨,先将卫星发射至近地圆轨道1上,然后在P处变轨到椭圆轨道2上,最后由轨道2在Q处变轨进入圆轨道3,轨道1、2相切于P点,轨道2、3相切于Q点.忽略空气阻力和卫星质量的变化,则以下说法正确的是( )| A. | 该卫星从轨道1变轨到轨道2需要在P处减速 | |
| B. | 该卫星在轨道从轨道1到轨道2再到轨道3,机械能逐渐减小 | |
| C. | 该卫星在轨道3的动能小于在轨道1的动能 | |
| D. | 该卫星稳定运行时,在轨道3上经过Q点的加速度等于在轨道2上Q点的加速度 |
8.物体受到10N的力的作用,4s内在力的方向上位移2米,则这个力做的功及功率分别为( )
| A. | 20J、5W | B. | 20J、10W | C. | 40J、10W | D. | 40J、20W |
 如图所示,倾角为30°、高h的粗糙斜面,一质量为m的物块,在沿斜面向上的恒力F作用下,能匀速从斜面底端向上运动到顶端.若把此物块放在斜面顶端恰好静止,用2F的恒力沿斜面向下拉动,使其由静止向下滑动,求滑至底端时的动能EK.
如图所示,倾角为30°、高h的粗糙斜面,一质量为m的物块,在沿斜面向上的恒力F作用下,能匀速从斜面底端向上运动到顶端.若把此物块放在斜面顶端恰好静止,用2F的恒力沿斜面向下拉动,使其由静止向下滑动,求滑至底端时的动能EK. 如图所示,一个质量为m=2 kg的物体,初速度为$\sqrt{0.8}m/s$,受到水平方向成37°角斜向下方的推力F1=10N作用,在水平地面上移动了距离s1=2m后撤去推力,此后物体又滑行了s2=1.6m的距离后停止了运动.设物体与地面间的滑动摩擦力为它们间弹力的0.2倍,求:
如图所示,一个质量为m=2 kg的物体,初速度为$\sqrt{0.8}m/s$,受到水平方向成37°角斜向下方的推力F1=10N作用,在水平地面上移动了距离s1=2m后撤去推力,此后物体又滑行了s2=1.6m的距离后停止了运动.设物体与地面间的滑动摩擦力为它们间弹力的0.2倍,求: