题目内容
20.在“验证牛顿运动定律”的实验中,采用如图1所示的实验装置.小车及车中砝码的质量用M表示,盘及盘中砝码的质量用m表示,小车的加速度可由小车后拖动的纸带打上的点计算出.
①当M与m的大小关系满足M>>m时,才可以认为绳对小车的拉力大小等于盘及盘中砝码的重力.
②一组同学在做加速度与质量的关系实验时,保持盘及盘中砝码的质量一定,改变小车及车中砝码的质量,测出相应的加速度,采用图象法处理数据.为了比较容易地检查出加速度a与质量M的关系,应该作a与$\frac{1}{M}$的图象.
③如图2所示为甲同学根据测量数据作出的a-F图线,说明实验存在的问题是没有平衡摩擦力或平衡摩擦力不足.
④小车带动纸带通过电火花计时器,打出的部分计数点如图3所示.每相邻两点间还有四点未画出来,电火花计时器使用的是220V、T=0.02s的交流电,求:电火花计时器打第2个计数点时,小车的速度v2=0.49m/s,小车的加速度a=0.88m/s2.(结果保留两位有效数字)
分析 ①当小车质量远大于砝码与砝码盘的质量时可近似认为小车受到的拉力等于砝码与砝码盘的重力;
②应用牛顿第二定律分析答题;
③实验前要平衡摩擦力,不平衡摩擦力或平衡摩擦力不足,则小车受到的合力小于砝码与砝码盘的重力,a-F图象在F轴上有截距;
④应用匀变速直线运动的推论可以求出瞬时速度与加速度.
解答 解:①当小车质量远大于砝码与砝码盘的质量时可以近似认为小车受到的拉力等于砝码与砝码盘的重力,因此需要满足的条件是:M>>m;
②由牛顿第二定律:F=Ma可知:a=$\frac{F}{M}$,在F一定时a与$\frac{1}{M}$成正比,为直观地找出a与M的关系,可以作出a-$\frac{1}{M}$图象;
③由图2所示a-F图象可知,图象在F轴上有截距,说明小车受到的合力小于砝码和砝码盘的重力,这是由实验前没有平衡摩擦力或平衡摩擦力不足造成的;
④每相邻两点间还有四点未画出来,计数点间的时间间隔:t=0.02×5=0.1s,
做匀变速直线运动的物体在某段时间内的平均速度等于中间时刻的瞬时速度,则:v2=$\frac{{s}_{1}+{s}_{2}}{2t}$=$\frac{0.0447+0.0534}{2×0.1}$≈0.49m/s;
由匀变速直线运动的推论:△x=at2可知,加速度:a=$\frac{{s}_{4}-{s}_{1}+{s}_{5}-{s}_{2}+{s}_{6}-{s}_{3}}{9{t}^{2}}$=$\frac{0.0710-0.0447+0.0800-0.0534+0.0886-0.0621}{9×0.{1}^{2}}$≈0.88m/s2.
故答案为:①M>>m;②$\frac{1}{M}$;③没有平衡摩擦力或平衡摩擦力不足;④0.49;0.88.
点评 本题考查了实验注意事项、实验数据处理、求瞬时速度与加速度问题,知道实验注意事项、掌握牛顿第二定律是解题的前提,应用匀变速直线运动的推论可以解题.

 如图所示,有两个穿着溜冰鞋的人站在冰面上,当其中一个人A从背后轻轻推另一个人B时,两个人都会向相反方向运动,这是因为A推B时( )
如图所示,有两个穿着溜冰鞋的人站在冰面上,当其中一个人A从背后轻轻推另一个人B时,两个人都会向相反方向运动,这是因为A推B时( )| A. | A与B之间有相互作用力 | |
| B. | A对B的作用在先,B对A的作用在后 | |
| C. | B对A的作用力大小等于A对B的作用力大小 | |
| D. | A对B的作用力和B对A的作用力是一对平衡力 |
| A. | 导体的电阻$R=ρ\frac{l}{s}$ | B. | 加速度a=$\frac{F}{m}$ | ||
| C. | 电场强度E=k$\frac{Q}{{r}^{2}}$ | D. | 电容器的电容$C=\frac{Q}{U}$ |
 如图所示,小球沿足够长的斜面向上做匀变速运动,依次经a、b、c、d到达最高点e.已知ab=bd=6m,bc=1m,小球从a到c和从c到d所用的时间都是2s,设小球经b、c时的速度分别为vb、vc,则( )
如图所示,小球沿足够长的斜面向上做匀变速运动,依次经a、b、c、d到达最高点e.已知ab=bd=6m,bc=1m,小球从a到c和从c到d所用的时间都是2s,设小球经b、c时的速度分别为vb、vc,则( )| A. | vb=$\sqrt{8}$ m/s | B. | vc=6 m/s | ||
| C. | xde=3 m | D. | 从d到e所用时间为4 s |
 如图所示,一个厚度不计的圆环A,紧套在长度为L的圆柱体B的上端,A、B两者的质量均为m.A与B之间的最大静摩擦力与滑动摩擦力相同,其大小为kmg(k>1).A、B由离地H高处由静止开始落下,触地后能竖直向上弹起,触地时间极短,且能量损失,A环运动过程中未落地.则下列说法正确的是( )
如图所示,一个厚度不计的圆环A,紧套在长度为L的圆柱体B的上端,A、B两者的质量均为m.A与B之间的最大静摩擦力与滑动摩擦力相同,其大小为kmg(k>1).A、B由离地H高处由静止开始落下,触地后能竖直向上弹起,触地时间极短,且能量损失,A环运动过程中未落地.则下列说法正确的是( )| A. | B与地第一次碰撞后,B上升的最大高度是$\frac{H}{k+1}$ | |
| B. | B与地第一次碰撞后,B上升的最大高度是$\frac{H}{k-1}$ | |
| C. | B与地第一次碰撞后,当A与B刚相对静止时,B离地面的高度是$\frac{H(k-1)}{{k}^{2}}$ | |
| D. | B与地第一次碰撞后,当A与B刚相对静止时,B离地面的高度是$\frac{H(k+1)}{{k}^{2}}$ |
 质量为M=4kg、长度l=$\frac{11}{8}$m的木板B,在水平恒定拉力F=10N作用下,以v0=2m/s的速度沿水平面做匀速直线运动.某时刻将质量为m=2kg的小物块A(可视为质点)由静止轻轻地放在木板的最右端,如图所示.小物块与木板间摩擦不计,重力加速度g取10m/s2.求:
质量为M=4kg、长度l=$\frac{11}{8}$m的木板B,在水平恒定拉力F=10N作用下,以v0=2m/s的速度沿水平面做匀速直线运动.某时刻将质量为m=2kg的小物块A(可视为质点)由静止轻轻地放在木板的最右端,如图所示.小物块与木板间摩擦不计,重力加速度g取10m/s2.求: 为了使航天员能适应在失重环境下的工作和生活,国家航天局组织对航天员进行失重训练.现利用训练客机创造一种失重环境.训练客机沿30°倾角爬升到7000米高空后飞机向上拉起,沿竖直方向以200m/s 的初速度向上作匀减速直线运动,匀减速的加速度为g,当飞机到最高点后立即掉头向下,仍沿竖直方向以加速度为g加速运动,当飞机离地3000米高时为了安全必须拉起,后又可一次次重复为航天员失重训练.为了防止飞机发生失速危险,每次飞机速度达到350m/s 后必须终止失重训练.请计算飞机一次上下运动为航天员创造的完全失重的时间.(g=10m/s2,结果保留一位小数)
为了使航天员能适应在失重环境下的工作和生活,国家航天局组织对航天员进行失重训练.现利用训练客机创造一种失重环境.训练客机沿30°倾角爬升到7000米高空后飞机向上拉起,沿竖直方向以200m/s 的初速度向上作匀减速直线运动,匀减速的加速度为g,当飞机到最高点后立即掉头向下,仍沿竖直方向以加速度为g加速运动,当飞机离地3000米高时为了安全必须拉起,后又可一次次重复为航天员失重训练.为了防止飞机发生失速危险,每次飞机速度达到350m/s 后必须终止失重训练.请计算飞机一次上下运动为航天员创造的完全失重的时间.(g=10m/s2,结果保留一位小数)
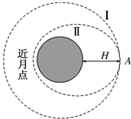 我国于2013年12月发射了“嫦娥三号”卫星,该卫星在距月球表面H处的环月轨道Ⅰ上做匀速圆周运动,其运行的周期为T,随后“嫦娥三号”在该轨道上A点采取措施,降至近月点高度为h的椭圆轨道Ⅱ上,如图所示.若以R表示月球的半径,忽略月球自转及地球对卫星的影响,万有引力常量为G,求:
我国于2013年12月发射了“嫦娥三号”卫星,该卫星在距月球表面H处的环月轨道Ⅰ上做匀速圆周运动,其运行的周期为T,随后“嫦娥三号”在该轨道上A点采取措施,降至近月点高度为h的椭圆轨道Ⅱ上,如图所示.若以R表示月球的半径,忽略月球自转及地球对卫星的影响,万有引力常量为G,求: