题目内容
如图所示，Ⅰ、Ⅱ、Ⅲ为电场和磁场的理想边界，一束电子（电量为e，质量为m，重力不计）由静止状态从P点经过Ⅰ、Ⅱ间的电场加速后垂直到达边界Ⅱ的Q点。匀强磁场的磁感应强度为B，磁场边界宽度为d，电子从磁场边界Ⅲ穿出时的速度方向与电子原来的入射方向夹角为30°。求：
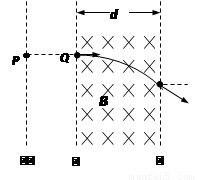
（1）电子在磁场中运动的时间t；
（2）若改变PQ间的电势差，使电子刚好不能从边界Ⅲ射出，则此时PQ间的电势差U是多少？
【答案】
（1）
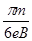（2）
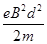
【解析】
试题分析：（1）电子在磁场中做匀速圆周运动
由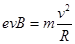
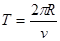
得电子在磁场中运动周期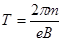
由题知粒子在磁场中转过的圆心角为30°
电子在磁场中运动时间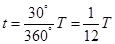
则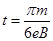
（2）电子刚好不从边界Ⅲ穿出时轨迹与边界相切，由几何关系知，
运动半径为R=d
由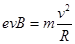
得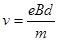
PQ间加速由动能定理有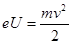
得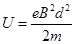
考点：带电粒子在组合场中的运动
点评：本题是带电粒子在加速电场和磁场中的运动。要能正确画出粒子运动的轨迹，并根据几何关系求得轨道半径，能用向心力公式和周期公式解题。
练习册系列答案
相关题目
如图所示，用长为L的细线拴一个质量为M的小球，使小球在水平面内做匀速圆周运动，细线与竖直方向间的夹角为θ，关于小球的受力情况，下列说法错误的是（ ）
如图所示是物体做匀变速直线运动得到的一条纸带，从O点开始每5个计时点取一个记数点，依照打点的先后顺序依次编为1、2、3、4、5、6，测得s1=5.18cm，s2=4.40cm，s3=3.62cm，s4=2.84cm，s5=2.06cm，s6=1.28cm．已知交流电源的频率为50Hz，
一木块静止在水平面上，质量m=2kg，与水平面间的动摩擦因数为0.2，受到按如图所示规律变化的水平拉力作用 （g=10m/s2） 求：
2008年9月我国成功发射了“神州七号”载人飞船．为了观察“神舟七号”的运行和宇航员仓外活动情况，飞船利用弹射装置发射一颗“伴星”．伴星经调整后，和“神舟七号”一样绕地球做匀速圆周运动，但比“神舟七号”离地面稍高一些，如图所示，那么（ ）