题目内容
14.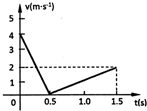 将质量m=2kg的小物块从斜面底端以一定的初速度沿斜面向上滑出,斜面上的速度传感器可以在计算机屏幕上得到其速度大小随时间的变化关系图象如图所示,求:
将质量m=2kg的小物块从斜面底端以一定的初速度沿斜面向上滑出,斜面上的速度传感器可以在计算机屏幕上得到其速度大小随时间的变化关系图象如图所示,求:(1)物块上滑和下滑的加速度a1、a2.
(2)斜面的倾角θ及物块与斜面间的动摩擦因数μ;
(3)物块从开始到再次回到斜面底端时,克服摩擦所产生的热能Q.
分析 (1)根据速度时间图线,根据图线的斜率分别求出上滑和下滑的加速度大小.
(2)根据上滑和下滑的加速度大小,根据牛顿第二定律列出表达式,从而得出斜面的倾角和摩擦因数.
(3)根据v-t图象求解走过位移,结合摩擦力做功公式求解.
解答 解:(1)物块上滑的加速度大小a1=$\frac{△{v}_{1}}{△{t}_{1}}$=$\frac{4}{0.5}$=8m/s2
物块下滑的加速度大小a2=$\frac{△{v}_{2}}{△{t}_{2}}$=$\frac{2}{1}$=2m/s2
(2)设物块质量为m,物块与斜面间的滑动摩擦系数为μ 则有:
ma1=mgsinθ+μmgcosθ
ma2=mgsinθ-μmgcosθ
联立解得:θ=30° μ=$\frac{\sqrt{3}}{5}$
(3)有图象可得,物块从开始到再次回到斜面底端时,走过位移为,x=S面=$\frac{1}{2}×4×0.5+\frac{1}{2}×2×1=2m$
根据功能关系,摩擦力做功转化为热量,Q=W摩=fx=$μmgcosθx=\frac{\sqrt{3}}{5}×2×10×\frac{\sqrt{3}}{2}×2$=12J
答:(1)物块上滑和下滑的加速度大小分别为8m/s2、2m/s2.
(2)斜面的倾角θ为30°摩擦因数=$\frac{\sqrt{3}}{5}$
(3)物块从开始到再次回到斜面底端时,克服摩擦所产生的热能Q为12J.
点评 解决本题的关键能够从图线中获取信息,知道图线的斜率表示加速度,图线与时间轴所围成的面积表示位移,摩擦力做功等于产生的热量.

 习题精选系列答案
习题精选系列答案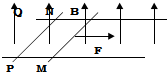 如图所示,两条足够长的光滑平行金属导轨水平放置导轨上,静止地放置两根质量相同、电阻相同的导体棒MN和PQ,两导体棒平行且垂直导轨,整个空间存在垂直于导轨平面的匀强磁场,不计导轨电阻,现在导体棒MN上施加一恒定的水平外力F,沿导轨向右运动,则下列说法正确的是( )
如图所示,两条足够长的光滑平行金属导轨水平放置导轨上,静止地放置两根质量相同、电阻相同的导体棒MN和PQ,两导体棒平行且垂直导轨,整个空间存在垂直于导轨平面的匀强磁场,不计导轨电阻,现在导体棒MN上施加一恒定的水平外力F,沿导轨向右运动,则下列说法正确的是( )| A. | 最终两导体棒都做匀速直线运动 | |
| B. | 最终两导体棒都做匀加速直线运动 | |
| C. | 导体棒MN上的电流一直增大 | |
| D. | 导体棒PQ上的电流先不断增大后保持不变 |
 如图甲所示,一倾角为37°的传送带以恒定速度运行,现将一质量m=1kg的小物块滑上传送带,物体相对地面的速度随时间变化的关系如图乙所示,取沿传送带向上为正方向,g=10m/s2,sin37°=0.6,cos37°=0.8.则下列说法正确的是 ( )
如图甲所示,一倾角为37°的传送带以恒定速度运行,现将一质量m=1kg的小物块滑上传送带,物体相对地面的速度随时间变化的关系如图乙所示,取沿传送带向上为正方向,g=10m/s2,sin37°=0.6,cos37°=0.8.则下列说法正确的是 ( )| A. | 0~8s内物体位移的大小为18m | |
| B. | 物体与传送带间的动摩擦因数为0.875 | |
| C. | 0~8s内传送带因运送物体而多做的功为216J | |
| D. | 0~8s内物体与传送带由于摩擦产生的热量为70J |
 如图,在水平地面上固定一倾角为θ的光滑绝缘斜面,斜面处于电场强度大小为E、方向沿斜面向下的匀强电场中.一劲度系数为k的绝缘轻质弹簧的一端固定在斜面底端,整根弹簧处于自然状态.一质量为m、带电量为q(q>0)的滑块从距离弹簧上端为s0处静止释放,滑块在运动过程中电量保持不变,设滑块与弹簧接触后粘在一起不分离且无机械能损失,物体刚好返回到s0段中点,弹簧始终处在弹性限度内,重力加速度为g.则( )
如图,在水平地面上固定一倾角为θ的光滑绝缘斜面,斜面处于电场强度大小为E、方向沿斜面向下的匀强电场中.一劲度系数为k的绝缘轻质弹簧的一端固定在斜面底端,整根弹簧处于自然状态.一质量为m、带电量为q(q>0)的滑块从距离弹簧上端为s0处静止释放,滑块在运动过程中电量保持不变,设滑块与弹簧接触后粘在一起不分离且无机械能损失,物体刚好返回到s0段中点,弹簧始终处在弹性限度内,重力加速度为g.则( )| A. | 滑块从静止释放到与弹簧上端接触瞬间所经历的时间为t1=$\sqrt{\frac{2m{s}_{0}}{qE+mgsinθ}}$ | |
| B. | 滑块运动过程中的最大动能等于(mgsinθ+qE)($\frac{mgsinθ+qE}{k}$+s0) | |
| C. | 弹簧的最大弹性势能为(mgsinθ+qE)s0 | |
| D. | 运动过程中滑块与弹簧系统机械能和电势能的总和始终保持不变 |
 为验证向心力公式,某探究小组设计了如图所示的演示实验,在米尺的一端钻一个小孔,使小孔恰能穿过一根细线,线下端挂一可视为质点,质量为m.将米尺固定在水平桌面上,测量出悬点到钢球的细线长度l,使钢球在水平面内做匀速圆周运动,圆心为O,待钢球的运动稳定后,用眼睛从米尺上方垂直于米尺往下看,读出钢球外侧到O点的距离r,并用秒表测量出钢球转动n圈用的时间t.则:
为验证向心力公式,某探究小组设计了如图所示的演示实验,在米尺的一端钻一个小孔,使小孔恰能穿过一根细线,线下端挂一可视为质点,质量为m.将米尺固定在水平桌面上,测量出悬点到钢球的细线长度l,使钢球在水平面内做匀速圆周运动,圆心为O,待钢球的运动稳定后,用眼睛从米尺上方垂直于米尺往下看,读出钢球外侧到O点的距离r,并用秒表测量出钢球转动n圈用的时间t.则:

 如图,A、B两物体叠放在一起,由静止释放后沿光滑固定斜面下滑,下滑过程中A、B始终保持相对静止,B上表面水平,则物体B的受力示意图是( )
如图,A、B两物体叠放在一起,由静止释放后沿光滑固定斜面下滑,下滑过程中A、B始终保持相对静止,B上表面水平,则物体B的受力示意图是( )


