题目内容
9. 在验证机械能守恒定律的实验中,质量为0.20kg的重物拖着纸带自由下落,在纸带上打出一系列的点,如图所示,已知相邻计数点间的时间间隔为0.02秒,当地的重力加速度为9.8m/s2,回答以下为题.
在验证机械能守恒定律的实验中,质量为0.20kg的重物拖着纸带自由下落,在纸带上打出一系列的点,如图所示,已知相邻计数点间的时间间隔为0.02秒,当地的重力加速度为9.8m/s2,回答以下为题.(1)纸带的左(选填“左”或“右”)端与重物相连;
(2)打点计时器应接交流(选填“直流”或“交流”)电源,实验时应先接通电源(填“释放纸带”或“接通电源”)
(3)从起点P到打下计数点B的过程中物体的重力势能减少量△Ep=0.400J,此过程中物体动能的增加量△Ek=0.388J;(结果保留3位有效数字)
(4)在上述验证机械能守恒定律的实验中发现,重锤减小的重力势能大于重锤动能的增加,其原因是由于在重锤下落的过程中存在阻力作用,通过以上实验数据可以测出重锤在下落过程中受到的平均阻力大小F=0.06N.(结果保留1位有效数字)
分析 纸带法实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的瞬时速度和加速度,从而求出动能.根据功能关系得重力势能减小量等于重力做功的数值.应用打点计时器时,要先接通电源,然后再放开纸带.根据牛顿第二定律求出阻力的大小.
解答 解:(1)从纸带上可以看出P点为先打出来的点,重物自由下落,而与重物相连的纸带在下端,应该先打点.所以纸带的左端应与重物相连.
(2)打点计时器应接交流电源,应用打点计时器时,要先接通电源,然后再放开纸带,
如果先释放纸带后接通电源,有可能会出现小车已经拖动纸带运动一段距离,电源才被接通,那么纸带上只有很小的一段能打上点,大部分纸带没有打上点,纸带的利用率太低.所以应当先接通电源,待打点稳定后再放开动纸带.
(3)重力势能减小量△Ep=mgh=0.2×9.8×0.2043J=0.400J.
利用匀变速直线运动的推论:
vB=$\frac{0.2456-0.1668}{2×0.02}$=1.97m/s
动能增加量△Ek=$\frac{1}{2}$mvB2=$\frac{1}{2}×0.2×1.9{7}^{2}$=0.388J.
(4)根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小,
得:xBC-xAB=aT2
a=$\frac{0.2456-0.2043-(0.2043-0.1668)}{0.0{2}^{2}}$=9.5m/s2
根据牛顿第二定律得,mg-F=ma
受到的平均阻力大小F=mg-ma=0.2×9.8-0.2×9.5=0.06N
故答案为:(1)左;(2)交流,接通电源; (3)0.400,0.388; (4)0.06.
点评 纸带问题的处理是力学实验中常见的问题.在纸带法实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的瞬时速度,计算过程中要注意单位的换算.

 图甲为一列简谐横波在t=2s时的波形图,图乙为介质中平衡位置在x=2m处的质点的振动图象,P、Q分别是平衡位置为x=1.5m和x=3.5m的质点.则下列说法正确的是( )
图甲为一列简谐横波在t=2s时的波形图,图乙为介质中平衡位置在x=2m处的质点的振动图象,P、Q分别是平衡位置为x=1.5m和x=3.5m的质点.则下列说法正确的是( )| A. | 波的传播方向向左 | B. | 波速为1m/s | ||
| C. | 质点P、Q运动的速度大小始终相等 | D. | 0~2s内,质点Q沿y轴正方向运动 | ||
| E. | 2~3s内,质点P运动的路程为4cm |
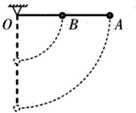 如图所示,一长为L的轻质细杆可绕其一端O点的竖直平面内自由转动,在杆的中点和另一端分别固定两个质量均为m的可看作质点的A、B小球.重力加速度为g,不计空气阻力.现将杆从水平位置静止释放,从开始运动到杆刚好转动到竖直位置的过程中,下列说法正确的是( )
如图所示,一长为L的轻质细杆可绕其一端O点的竖直平面内自由转动,在杆的中点和另一端分别固定两个质量均为m的可看作质点的A、B小球.重力加速度为g,不计空气阻力.现将杆从水平位置静止释放,从开始运动到杆刚好转动到竖直位置的过程中,下列说法正确的是( )| A. | B球机械能守恒 | |
| B. | A球运动到最低点时,重力的功率为2mg$\sqrt{\frac{3gL}{5}}$ | |
| C. | B球到达最低点时的速度为$\sqrt{\frac{3gL}{5}}$ | |
| D. | 细杆对A球做功为$\frac{1}{5}$mgL |
| A. | 公式只适用于轨道是椭圆的运动 | |
| B. | 公式中的T为天体的自转周期 | |
| C. | 公式中的k值,只与中心天体有关,与绕中心天体公转的行星(或卫星)无关 | |
| D. | 若已知月球与地球之间的距离,根据开普勒第三定律公式可求出地球与太阳之间的距离 |
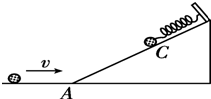 如图所示,光滑斜面的顶端固定一弹簧,一小球向右滑行,并冲上固定在地面上的斜面.设小球在斜面最低点A的速度为V,压缩弹簧至C点时弹簧最短,C点距地面高度为h,则从A到C的过程中弹簧弹性势能的增加量是( )
如图所示,光滑斜面的顶端固定一弹簧,一小球向右滑行,并冲上固定在地面上的斜面.设小球在斜面最低点A的速度为V,压缩弹簧至C点时弹簧最短,C点距地面高度为h,则从A到C的过程中弹簧弹性势能的增加量是( )| A. | mgh-$\frac{1}{2}$mv2 | B. | $\frac{1}{2}$mv2-mgh | C. | -mgh | D. | -[mgh+$\frac{1}{2}$mv2] |
 如图所示,A、B、C是在地球大气层外圆形轨道上运动的3颗卫星,已知mA=mB>mC,下列说法正确的是( )
如图所示,A、B、C是在地球大气层外圆形轨道上运动的3颗卫星,已知mA=mB>mC,下列说法正确的是( )| A. | 角速度大小的关系是ωA>ωB=ωC | B. | 周期关系是TA>TB=TC | ||
| C. | 向心力大小的关系是FA=FB>FC | D. | 向心加速度大小的关系是aA<aB=aC |

| A. | 甲段电路的电阻比乙段电路的电阻较大 | |
| B. | 甲段电路两端的电压比乙段两端电压较大 | |
| C. | 将两导线串联,甲段电路分得的电压较低 | |
| D. | 将两段导线并联,乙段电路获得的电压功率较大 |
