��Ŀ����
16�� �ڡ���֤��е���غ㶨�ɡ���ʵ���У�����Ϊm���ش�����ֽ�����䣬�ڴ˹����У�����ʱ����ֽ���ϴ��һϵ�еĵ㣬��ֽ����ѡȡ 5�����ڼ�����A��B��C��D��E�����ڼ�����ʱ����Ϊ T������OΪ�ش���ʼ����ʱ��¼�ĵ㣬��������֮��ľ�����ͼ��ʾ���������������ٶ�Ϊg��
�ڡ���֤��е���غ㶨�ɡ���ʵ���У�����Ϊm���ش�����ֽ�����䣬�ڴ˹����У�����ʱ����ֽ���ϴ��һϵ�еĵ㣬��ֽ����ѡȡ 5�����ڼ�����A��B��C��D��E�����ڼ�����ʱ����Ϊ T������OΪ�ش���ʼ����ʱ��¼�ĵ㣬��������֮��ľ�����ͼ��ʾ���������������ٶ�Ϊg����1������ʱ�����¼�����Bʱ���ش�������ٶ� vB=$\frac{{s}_{1}+{s}_{2}}{2T}$������ʱ�����¼�����Dʱ���ش�������ٶ�vD=$\frac{{s}_{3}+{s}_{4}}{2T}$��
��2���Ӵ��¼�����B�����¼�����D�Ĺ����У��ش��Ķ�����������EK=$\frac{m����{s}_{3}+{s}_{4}��^{2}-��{s}_{1}+{s}_{2}��^{2}��}{8{T}^{2}}$
��3���Ӵ��¼�����B�����¼�����D�Ĺ����У��ش����������ܼ�С����EP=mg��s2+s3���������������Χ�ڣ�ͨ���Ƚϡ�EK�͡�EP�Ϳ�����֤�ش���������л�е���غ��ˣ�
���� ���ʵ����������Ҫ���ո�ʵ��ԭ�����˽�ʵ���������������������ݴ����Լ�ע�����
ֽ����ʵ���У���ֽ���ȱ���ֱ���˶������ֽ���ϵĵ��࣬�����ȱ���ֱ���˶������ۣ��ɼ�������ij��ʱֽ���˶���˲ʱ�ٶȺͼ��ٶȣ��Ӷ�������ܣ����ݹ��ܹ�ϵ���������ܼ�С������������������ֵ
��� �⣺��1���������ȱ���ֱ���˶�������
vB=$\frac{{x}_{AC}}{{t}_{AC}}$=$\frac{{s}_{1}+{s}_{2}}{2T}$
vD=$\frac{{x}_{CE}}{{t}_{CE}}$=$\frac{{s}_{3}+{s}_{4}}{2T}$
��2���Ӵ��¼�����B�����¼�����D�Ĺ����У��ش��Ķ���������Ϊ��
��EK=EkD-EkB=$\frac{1}{2}$mvD2-$\frac{1}{2}$mvB2=$\frac{m����{s}_{3}+{s}_{4}��^{2}-��{s}_{1}+{s}_{2}��^{2}��}{8{T}^{2}}$
��3�������������ܵĶ���ʽ���Ӵ��¼�����B�����¼�����D�Ĺ����У��ش��������ܼ�С��Ϊ��
��EP=mgh=mg��s2+s3����
�ʴ�Ϊ����1��$\frac{{s}_{1}+{s}_{2}}{2T}$��$\frac{{s}_{3}+{s}_{4}}{2T}$����2��$\frac{m����{s}_{3}+{s}_{4}��^{2}-��{s}_{1}+{s}_{2}��^{2}��}{8{T}^{2}}$����3��mg��s2+s3����
���� �����˶�ѧ��ʽ�Ͷ��ܡ��������ܵĶ���ʽ��������Ǹ�ʵ��ij������⣮
������ĸ������Ҫϸ�ĵ㣮

 Ӧ������ҵ��ϵ�д�
Ӧ������ҵ��ϵ�д�| A�� | ��������������ʱ����������һ�������� | |
| B�� | ��������������ʱ����������Ҳ������ | |
| C�� | ������������ʱ����������Ҳ���������� | |
| D�� | �������뷴�����������Ĺ�һ���Ǵ�С��� |
 ��ͼ��ʾ������Բ��״�Ļ�ת�������ݣ������������ڹ⻬���������Խ��ٶȦؿ�����ת��ͬʱ���ٶ�v�����˶�������ת������һֱ������ֱ��Ϊʹ��ת�������ӵı�Ե����ʱ���������ӱ�Ե������ײ���ٶ�v����Ӧ���ڣ����ת���ĸ�ΪH������뾶ΪR�����ƿ����Ի�ת�������ã���������
��ͼ��ʾ������Բ��״�Ļ�ת�������ݣ������������ڹ⻬���������Խ��ٶȦؿ�����ת��ͬʱ���ٶ�v�����˶�������ת������һֱ������ֱ��Ϊʹ��ת�������ӵı�Ե����ʱ���������ӱ�Ե������ײ���ٶ�v����Ӧ���ڣ����ת���ĸ�ΪH������뾶ΪR�����ƿ����Ի�ת�������ã���������| A�� | ��R | B�� | R$\sqrt{\frac{g}{2H}}$ | C�� | R$\sqrt{\frac{2g}{H}}$ | D�� | ��H |
| A�� | P | B�� | P-$\frac{{P}^{2}}{{U}^{2}}$•r | C�� | P-$\frac{{U}^{2}}{r}$ | D�� | $\frac{{P}^{2}}{{U}^{2}}$•r |

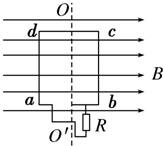 ��ͼ��ʾ��������Ȧabcd�ڴŸ�Ӧǿ��B=2T����ǿ�ų�������OO���Խ��ٶȦ�=10�� rad/s�Ƚ���ת������Ȧ��10�ѣ���Ȧ�ܵ���r=5����ab=0.3m��bc=0.6m�����ص���R=45������
��ͼ��ʾ��������Ȧabcd�ڴŸ�Ӧǿ��B=2T����ǿ�ų�������OO���Խ��ٶȦ�=10�� rad/s�Ƚ���ת������Ȧ��10�ѣ���Ȧ�ܵ���r=5����ab=0.3m��bc=0.6m�����ص���R=45������ ��ͼ��ʾ����xoy���ڣ���һ����������ǿ�糡����ǿ��СΪE������ ��y����������X����·�����ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB������ֱֽ���������һ������Ϊm �����Ϊq�Ĵ���������ӣ��������ӵ����������� ����������y���ϵ�P���Գ��ٶ�V0��ֱ�ڵ糡���� ���˵糡�����糡ƫת��������X�������30����� �ų�������ɣ�
��ͼ��ʾ����xoy���ڣ���һ����������ǿ�糡����ǿ��СΪE������ ��y����������X����·�����ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB������ֱֽ���������һ������Ϊm �����Ϊq�Ĵ���������ӣ��������ӵ����������� ����������y���ϵ�P���Գ��ٶ�V0��ֱ�ڵ糡���� ���˵糡�����糡ƫת��������X�������30����� �ų�������ɣ�