题目内容
4. 如图,有一质量为2kg的物体放在长为1m的斜面顶部,斜面倾角θ=37°.
如图,有一质量为2kg的物体放在长为1m的斜面顶部,斜面倾角θ=37°.(1)若由静止释放物体,1s后物体到达斜面底端,则物体到达斜面底端时的速度大小为多少?
(2)物体与斜面之间的动摩擦因数为多少?
(3)若给物体施加一个竖直方向的恒力,使其由静止释放后沿斜面向下做加速度大小
为1.5m/s2的匀加速直线运动,则该恒力大小为多少?
分析 (1)根据平均速度公式$\overline{v}$=$\frac{x}{t}$=$\frac{{v}_{0}+v}{2}$可求得物体到达底部的速度大小;
(2)根据速度公式可求得加速度,再根据牛顿第二定律可求得动摩擦因数大小;
(3)对物体进行受力分析,根据牛顿第二定律可求得恒力的大小.
解答 解:
(1)根据平均速度公式可知:
s=$\frac{1}{2}$vt,
解得:v=$\frac{2s}{t}$=$\frac{2×1}{1}$ m/s=2m/s
(2)根据速度公式可知:a1=$\frac{v}{t}$=$\frac{2}{1}$ m/s2=2 m/s2,
由牛顿第二定律得:mgsinθ-μmgcosθ=ma1,
将a1=$\frac{v}{t}$=$\frac{2}{1}$ m/s2=2 m/s2,θ=37°代入,
可求得μ=0.5
(3)因为物体加速度向下,所以恒力F与重力的合力竖直向下,设该合力为F竖,
则有F竖sinθ-μF竖cosθ=ma2
将a2=1.5 m/s2、θ=37°、μ=0.5代入,可求得F竖=15N
因为F竖=mg-F,所以F=mg-F竖=20N-15N=5N
答:(1)若由静止释放物体,1s后物体到达斜面底端,则物体到达斜面底端时的速度大小为2m/s;
(2)物体与斜面之间的动摩擦因数为0.5;
(3)该恒力大小为5N.
点评 本题考查牛顿第二定律的综合应用,要注意正确进行受力分析和运动学过程分析,明确加速度在力和运动学中的桥梁作用.

练习册系列答案
相关题目
14. 如图是男子体操项目中的“单臂大回环”.运动员单手抓住单杠,伸展身体,从静止开始以单杠为轴做圆周运动.已知运动员质量为60kg,若忽略运动过程中空气阻力及手与单杠间摩擦,则运动员到达最低点时手臂所受拉力约为( )
如图是男子体操项目中的“单臂大回环”.运动员单手抓住单杠,伸展身体,从静止开始以单杠为轴做圆周运动.已知运动员质量为60kg,若忽略运动过程中空气阻力及手与单杠间摩擦,则运动员到达最低点时手臂所受拉力约为( )
 如图是男子体操项目中的“单臂大回环”.运动员单手抓住单杠,伸展身体,从静止开始以单杠为轴做圆周运动.已知运动员质量为60kg,若忽略运动过程中空气阻力及手与单杠间摩擦,则运动员到达最低点时手臂所受拉力约为( )
如图是男子体操项目中的“单臂大回环”.运动员单手抓住单杠,伸展身体,从静止开始以单杠为轴做圆周运动.已知运动员质量为60kg,若忽略运动过程中空气阻力及手与单杠间摩擦,则运动员到达最低点时手臂所受拉力约为( )| A. | 600N | B. | 2400N | C. | 3000N | D. | 3600N |
13.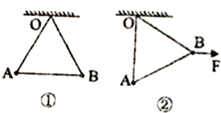 如图①所示,用OA、OB、AB三根轻质绝缘绳悬挂两个质量均为m带等量同种电荷的小球(可视为质点),三根绳子处于拉伸状态,且构成一个正三角形,AB绳水平,OA绳对小球的作用力大小为T.现用绝缘物体对右侧小球施加一水平拉力F,使装置静止在图②所示的位置,此时OA绳对小球的作用力大小为T'.根据以上信息可以判断T和T'的比值为( )
如图①所示,用OA、OB、AB三根轻质绝缘绳悬挂两个质量均为m带等量同种电荷的小球(可视为质点),三根绳子处于拉伸状态,且构成一个正三角形,AB绳水平,OA绳对小球的作用力大小为T.现用绝缘物体对右侧小球施加一水平拉力F,使装置静止在图②所示的位置,此时OA绳对小球的作用力大小为T'.根据以上信息可以判断T和T'的比值为( )
 如图①所示,用OA、OB、AB三根轻质绝缘绳悬挂两个质量均为m带等量同种电荷的小球(可视为质点),三根绳子处于拉伸状态,且构成一个正三角形,AB绳水平,OA绳对小球的作用力大小为T.现用绝缘物体对右侧小球施加一水平拉力F,使装置静止在图②所示的位置,此时OA绳对小球的作用力大小为T'.根据以上信息可以判断T和T'的比值为( )
如图①所示,用OA、OB、AB三根轻质绝缘绳悬挂两个质量均为m带等量同种电荷的小球(可视为质点),三根绳子处于拉伸状态,且构成一个正三角形,AB绳水平,OA绳对小球的作用力大小为T.现用绝缘物体对右侧小球施加一水平拉力F,使装置静止在图②所示的位置,此时OA绳对小球的作用力大小为T'.根据以上信息可以判断T和T'的比值为( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | ||
| C. | $\sqrt{3}$ | D. | 条件不足,无法确定 |
 如图所示,在一个光滑金属框架上垂直放置一根长l=0.4m的金属棒ab,其电阻r=0.1Ω.框架左端的电阻R=0.4Ω.垂直框面的匀强磁场的磁感强度B=0.1T.用外力使棒ab以速度v=5m/s向右匀速移动.求:
如图所示,在一个光滑金属框架上垂直放置一根长l=0.4m的金属棒ab,其电阻r=0.1Ω.框架左端的电阻R=0.4Ω.垂直框面的匀强磁场的磁感强度B=0.1T.用外力使棒ab以速度v=5m/s向右匀速移动.求: 如图所示一轻质弹簧下端固定,直立于水平地面上,将质量为1kg的物体A从离弹簧顶端正上方1m高处由静止释放,当物体A下降到最低点P时,其速度变为零,此时弹簧的压缩量为0.6m.(g=10m/s2)
如图所示一轻质弹簧下端固定,直立于水平地面上,将质量为1kg的物体A从离弹簧顶端正上方1m高处由静止释放,当物体A下降到最低点P时,其速度变为零,此时弹簧的压缩量为0.6m.(g=10m/s2)