题目内容
18.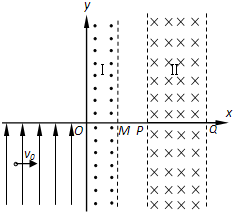 如图所示,在直角坐标系xoy的第一、四象限区域内存在两个有界的匀强磁场:垂直纸面向外的匀强磁场Ⅰ、垂直纸面向里的匀强磁场Ⅱ,O、M、P、Q为磁场边界和x轴的交点,OM=MP=L.在第三象限存在沿y轴正向的匀强电场.一质量为m带电量为+q的带电粒子从电场中坐标为(-4L,-2L)的点以速度v0沿+x方向射出,恰好经过原点O处射入区域Ⅰ又从M点射出区域Ⅰ(粒子的重力忽略不计).
如图所示,在直角坐标系xoy的第一、四象限区域内存在两个有界的匀强磁场:垂直纸面向外的匀强磁场Ⅰ、垂直纸面向里的匀强磁场Ⅱ,O、M、P、Q为磁场边界和x轴的交点,OM=MP=L.在第三象限存在沿y轴正向的匀强电场.一质量为m带电量为+q的带电粒子从电场中坐标为(-4L,-2L)的点以速度v0沿+x方向射出,恰好经过原点O处射入区域Ⅰ又从M点射出区域Ⅰ(粒子的重力忽略不计).(1)求第三象限匀强电场场强E的大小;
(2)求区域Ⅰ内匀强磁场磁感应强度B的大小;
(3)如带电粒子能再次回到原点O,问区域Ⅱ内磁场的宽度至少为多少?粒子两次经过原点O的时间间隔为多少?
分析 (1)带电粒子在匀强电场中做类平抛运动,运用运动的分解法,由牛顿第二定律和运动学公式求解场强E的大小;
(2)带电粒子进入磁场后,由洛伦兹力提供向心力做匀速圆周运动.由题意,粒子经过原点O处射入区域I又从M点射出区域I,画出轨迹,由几何知识求出轨迹半径,由牛顿第二定律即可求得磁感应强度B的大小;
(3)当带电粒子恰好能再次回到原点O,在磁场Ⅱ中轨迹恰好与其右边界相切,画出轨迹,由几何关系即可求出磁场的宽度.分段求出时间,即可求得总时间.
解答  解:(1)带电粒子在匀强电场中做类平抛运动.
解:(1)带电粒子在匀强电场中做类平抛运动.
水平方向:4L=v0t
竖直方向:2L=$\frac{1}{2}$$\frac{qE}{m}$($\frac{4L}{{v}_{0}}$)2
联立得:E=$\frac{m{{v}_{0}}^{2}}{4qL}$
(2)设到原点时带电粒子的竖直分速度为vy:
vy=$\frac{qE}{m}$t=$\frac{qE}{m}$$\frac{4L}{{v}_{0}}$=v0
方向与轴正向成 45°角 粒子进入区域Ⅰ做匀速圆周运动,由几何知识可得:
R1=$\frac{\sqrt{2}}{2}$L
由洛伦兹力充当向心力:Bqv=m$\frac{{v}^{2}}{{R}_{1}}$
可解得:B=$\frac{mv}{q{R}_{1}}$=$\frac{2mv}{qL}$
(3)运动轨迹如图,在区域Ⅱ做匀速圆周的半径为:R2=$\sqrt{2}$L
d2≥R2+L=($\sqrt{2}$+1)L
运动时间:粒子从O到M的运动时间t1=$\frac{\frac{π}{2}\frac{\sqrt{2}}{2}L}{\sqrt{2}{v}_{0}}$=$\frac{πL}{4{v}_{0}}$
粒子从M到N的运动时间t2=$\frac{\sqrt{2}L}{\sqrt{2}{v}_{0}}$=$\frac{L}{{v}_{0}}$
粒子在区域Ⅱ中的运动时间t3=$\frac{\frac{3π}{2}\sqrt{2}L}{\sqrt{2}{V}_{0}}$=$\frac{3πL}{2{v}_{0}}$
粒子两次经过原点O的时间间隔为:t总=2(t1+t2)+t3=$\frac{2(π+1)L}{{v}_{0}}$
答:(1)第三象限匀强电场场强E的大小为$\frac{m{{v}_{0}}^{2}}{4qL}$;
(2)区域Ⅰ内匀强磁场磁感应强度B的大小为$\frac{2mv}{qL}$;
(3)如带电粒子能再次回到原点O,问区域Ⅱ内磁场的宽度至少为($\sqrt{2}$+1)L,粒子两次经过原点O的时间间隔为$\frac{2(π+1)L}{{v}_{0}}$.
点评 本题考查带电粒子在电磁场中的运动,注意在磁场中的运动要注意几何关系的应用,在电场中注意由类平抛运动的规律求解.

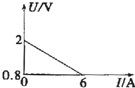 为研究问题方便,有时我们会把路端电压与干路电流的变化关系图象中I轴向上平移,使得图线“很快”便与I轴出现交点,如图所示.则由该图象可知( )
为研究问题方便,有时我们会把路端电压与干路电流的变化关系图象中I轴向上平移,使得图线“很快”便与I轴出现交点,如图所示.则由该图象可知( )| A. | 电源电动势为2V | |
| B. | 电源内阻为$\frac{1}{3}$Ω | |
| C. | 电源的短路电流为6A | |
| D. | 电路路端电压为1V时,电路中的电流为5A |
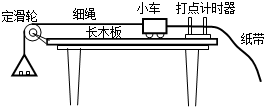
| A. | 先接通电源,后释放小车 | |
| B. | 调节定滑轮的高度,使细绳与长木板平行 | |
| C. | 用秒表测出小车运动的时间 | |
| D. | 将长木板右端垫高,平衡小车和纸带受到的摩擦力 |
 如图所示,一质量为m的物体在沿斜面向上的恒力F作用下,由静止从底端向上做匀加速直线运动.若斜面足够长,表面光滑,倾角为θ.经时间t,恒力F做功80J,此后撤去恒力F,物体又经时间t回到出发点,且回到出发点时的速度大小为v,若以地面为重力势能的零势能面,则下列说法中不正确的是( )
如图所示,一质量为m的物体在沿斜面向上的恒力F作用下,由静止从底端向上做匀加速直线运动.若斜面足够长,表面光滑,倾角为θ.经时间t,恒力F做功80J,此后撤去恒力F,物体又经时间t回到出发点,且回到出发点时的速度大小为v,若以地面为重力势能的零势能面,则下列说法中不正确的是( )| A. | 物体回到出发点时的机械能是80J | |
| B. | 在撤去力F前的瞬时,力F的功率大小是$\frac{2}{3}$mgvsinθ | |
| C. | 撤去力F前的运动过程中,物体的重力势能一直在增加 | |
| D. | 撤去力F后的运动过程中物体的动能一直在减少 |
| A. | 向上做匀加速运动 | B. | 向上做匀减速运动 | ||
| C. | 向下做匀加速运动 | D. | 向下做匀减速运动 |
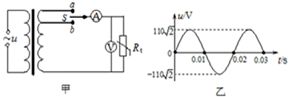 如图甲所示,理想变压器原线圈输入交流电压,副线圈中装有单刀双掷开关S,电流表、电压表均为理想电表,R0为热敏电阻,S掷a时原副线圈匝数比$\frac{{n}_{1}}{{n}_{2}}$=$\frac{2}{1}$,S掷b时原副线圈匝数比$\frac{{n}_{1}}{{n}_{2}}$=$\frac{11}{4}$,图乙为S掷a时变压器副线圈输出电压的波形,则以下分析正确的是( )
如图甲所示,理想变压器原线圈输入交流电压,副线圈中装有单刀双掷开关S,电流表、电压表均为理想电表,R0为热敏电阻,S掷a时原副线圈匝数比$\frac{{n}_{1}}{{n}_{2}}$=$\frac{2}{1}$,S掷b时原副线圈匝数比$\frac{{n}_{1}}{{n}_{2}}$=$\frac{11}{4}$,图乙为S掷a时变压器副线圈输出电压的波形,则以下分析正确的是( )| A. | S接在a端,电压表的示数为110$\sqrt{2}$V | |
| B. | 原线圈输入电压为220$\sqrt{2}$V | |
| C. | S接在b段,电压表的示数为80V | |
| D. | S接在a端,一段时间后电流表读数将不断变小 |
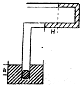 如图1所示,U形管处于竖直平面内,管内和水银槽内都有水银,外界大气压为为P0,两面水平管中水银长度差为H,竖直管内外水银面的高度差为H,则被封闭的气体压强为P0+ρgH.(水银的密度为ρ)
如图1所示,U形管处于竖直平面内,管内和水银槽内都有水银,外界大气压为为P0,两面水平管中水银长度差为H,竖直管内外水银面的高度差为H,则被封闭的气体压强为P0+ρgH.(水银的密度为ρ)