题目内容
2. 如图所示为某娱乐场的滑道示意图,其中AB为曲面滑道,BC为水平滑道,CD为$\frac{1}{4}$圆弧滑道,各滑道相切连接.DE为放在水平地面上的海绵垫.某人从A点上方某处滑下,经过高度差H=5m的A点和C点时的速度分别为2m/s和4m/s,在C点做平抛运动,最后落在海绵垫上E点.已知人的质量为50kg,人与水平滑道BC间的动摩擦因数为0.2,水平滑道BC的长度为s=20m,只知道圆弧CD的半径R的范围为:1m≤R≤2m.取g=10m/s2.求:
如图所示为某娱乐场的滑道示意图,其中AB为曲面滑道,BC为水平滑道,CD为$\frac{1}{4}$圆弧滑道,各滑道相切连接.DE为放在水平地面上的海绵垫.某人从A点上方某处滑下,经过高度差H=5m的A点和C点时的速度分别为2m/s和4m/s,在C点做平抛运动,最后落在海绵垫上E点.已知人的质量为50kg,人与水平滑道BC间的动摩擦因数为0.2,水平滑道BC的长度为s=20m,只知道圆弧CD的半径R的范围为:1m≤R≤2m.取g=10m/s2.求:(1)人在AB段克服阻力的功;
(2)人在C点做平抛运动的水平位移x的范围.
分析 (1)对A到B的过程运用动能定理,根据动能定理求出人克服阻力做的功.
(2)当人在C点对轨道的压力为零时,根据在C点重力提供向心力,之后做平抛运动,根据平抛运动的规律计算水平位移的大小关系.
解答 解:(1)设人从A点滑到C点过程中,重力做的功以及在水平段克服摩擦阻力的功和在AB段克服阻力的功分别为:WG、Wf和WAB.
由动能定理:WG-Wf-WAB=EKC-EKA
即:mgH-μmgs-WAB=$\frac{1}{2}$mvC2-$\frac{1}{2}$mvA2
代入数据得人在AB段克服阻力的功:WAB=200J.
(2)人在C点做平抛运动,有:mg≤m$\frac{{v}_{c}^{2}}{R}$,
解得:R≤$\frac{{v}_{c}^{2}}{g}$=1.6m
结合已知条件1m≤R≤1.6m由$R=\frac{1}{2}g{t}^{2}$可确定平抛运动的时间范围为:$\sqrt{\frac{1}{5}}s≤t≤\sqrt{\frac{1.6}{5}}s$
由x=vCt可确定平抛运动的水平位移x的范围为:$\frac{4\sqrt{5}}{5}m≤x≤\frac{8\sqrt{2}}{5}m$
答:(1)人在AB段克服阻力的功为200J;
(2)人在C点做平抛运动的水平位移x的范围为 $\frac{4\sqrt{5}}{5}m≤x≤\frac{8\sqrt{2}}{5}m$.
点评 本题是多过程问题,关键是理清运动过程,选择合适的规律,比如牛顿运动定律、动能定理进行求解.

练习册系列答案
相关题目
13. 如图所示,甲从高h处以速度v1平抛小球A,乙同时从地面以初速度V2竖直上抛小球B,在B尚未到达最高点之前,两球在空中相遇,则( )
如图所示,甲从高h处以速度v1平抛小球A,乙同时从地面以初速度V2竖直上抛小球B,在B尚未到达最高点之前,两球在空中相遇,则( )
 如图所示,甲从高h处以速度v1平抛小球A,乙同时从地面以初速度V2竖直上抛小球B,在B尚未到达最高点之前,两球在空中相遇,则( )
如图所示,甲从高h处以速度v1平抛小球A,乙同时从地面以初速度V2竖直上抛小球B,在B尚未到达最高点之前,两球在空中相遇,则( )| A. | 两球相遇时间$t=\frac{h}{v_2}$ | B. | 抛出前两球的水平距离$s=\frac{{{v_1}h}}{v_2}$ | ||
| C. | 相遇时A球的速率为$\frac{gh}{v_2}$ | D. | 若v2=$\sqrt{gh}$,则两球相遇在$\frac{h}{2}$ |
10.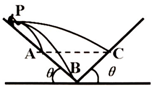 如图,在某一峡谷的两侧存在与水平面成相同角度的山坡,某人站在左侧山坡上的P点向对面山坡上水平抛出三个质量不等的石块,分别落在A、B、C三处,不计空气阻力,A、C两处在同一水平面上,则下列说法正确的是( )
如图,在某一峡谷的两侧存在与水平面成相同角度的山坡,某人站在左侧山坡上的P点向对面山坡上水平抛出三个质量不等的石块,分别落在A、B、C三处,不计空气阻力,A、C两处在同一水平面上,则下列说法正确的是( )
 如图,在某一峡谷的两侧存在与水平面成相同角度的山坡,某人站在左侧山坡上的P点向对面山坡上水平抛出三个质量不等的石块,分别落在A、B、C三处,不计空气阻力,A、C两处在同一水平面上,则下列说法正确的是( )
如图,在某一峡谷的两侧存在与水平面成相同角度的山坡,某人站在左侧山坡上的P点向对面山坡上水平抛出三个质量不等的石块,分别落在A、B、C三处,不计空气阻力,A、C两处在同一水平面上,则下列说法正确的是( )| A. | 落在C处的石块在空中运动的时间最长 | |
| B. | 落在A、B两处的石块落地速度方向相同 | |
| C. | 落在A、B、C三处的石块落地速度方向相同 | |
| D. | 落在B、C两处的石块落地速度大小一定不同 |
17.关于力做功的判断,下列说法正确的是( )
| A. | 只要物体受力且发生位移,则力对物体一定做功 | |
| B. | 如果一个力阻碍了物体的运动,则这个力一定对物体做负功 | |
| C. | 摩擦力一定对物体做负功 | |
| D. | 作用力做正功时,反作用力一定做负功 |
14. 一玻璃砖横截面如图所示,其中ABC为直角三角形(AC边未画出),AB为直角边,∠ABC═45°;ADC为一圆弧,其圆心在BC边的中点.此玻璃的折射率为1.5,P为一贴近玻璃砖放置的与边垂直的光屏.若一束宽度与AB边长度相等的平行光从AB边垂直射入玻璃砖,则( )
一玻璃砖横截面如图所示,其中ABC为直角三角形(AC边未画出),AB为直角边,∠ABC═45°;ADC为一圆弧,其圆心在BC边的中点.此玻璃的折射率为1.5,P为一贴近玻璃砖放置的与边垂直的光屏.若一束宽度与AB边长度相等的平行光从AB边垂直射入玻璃砖,则( )
 一玻璃砖横截面如图所示,其中ABC为直角三角形(AC边未画出),AB为直角边,∠ABC═45°;ADC为一圆弧,其圆心在BC边的中点.此玻璃的折射率为1.5,P为一贴近玻璃砖放置的与边垂直的光屏.若一束宽度与AB边长度相等的平行光从AB边垂直射入玻璃砖,则( )
一玻璃砖横截面如图所示,其中ABC为直角三角形(AC边未画出),AB为直角边,∠ABC═45°;ADC为一圆弧,其圆心在BC边的中点.此玻璃的折射率为1.5,P为一贴近玻璃砖放置的与边垂直的光屏.若一束宽度与AB边长度相等的平行光从AB边垂直射入玻璃砖,则( )| A. | 屏上有一亮区,其宽度小于AB边的长度 | |
| B. | 屏上有一亮区,其宽度等于AC边的长度 | |
| C. | 从BC边折射出一束宽度与BC边长度相等的平行光 | |
| D. | 当屏向远离玻璃砖的方向平行移动时,屏上亮区先逐渐变小然后逐渐变大 |
11.为了确定某星球的密度与地球密度的关系,宇航员在该星球表面做了一些测试,若测得该星球的自转周期为T,一探测器在该星球两极处所受的重力为P,在该星球赤道处所受的重力为kP(k<1),假设该星球和地球均是质量分布均匀的球体,一卫星在地球表面附近绕地球做圆周运动的周期为nT(n>1),则该星球密度与地球密度的比值为( )
| A. | $\frac{{n}^{2}}{1-k}$ | B. | $\frac{{n}^{2}}{1+k}$ | C. | $\frac{n}{1-k}$ | D. | $\frac{n}{1+k}$ |
10.在光电效应的实验中,能够增大光电子最大初动能的有效方法是( )
| A. | 增大入射光的强度 | B. | 增大入射光的频率 | ||
| C. | 延长入射光的照射时间 | D. | 换一块逸出功较大的金属板 |
 如图所示,AB为竖直转轴,细绳AC和BC的结点C系一质量为m的小球,两绳能承担的最大拉力均为2mg,当AC和BC均拉直时∠ABC=90°,∠ACB=53°,ABC能绕竖直轴AB匀速转动,因而C球在水平面内做匀速圆周运动,求:
如图所示,AB为竖直转轴,细绳AC和BC的结点C系一质量为m的小球,两绳能承担的最大拉力均为2mg,当AC和BC均拉直时∠ABC=90°,∠ACB=53°,ABC能绕竖直轴AB匀速转动,因而C球在水平面内做匀速圆周运动,求: