题目内容
 如图,质量分别为m和M的两个星球A和B在引力作用下都绕O点做匀速圆周运动,星球A和B两者中心之间的距离为L.已知A、B的中心和O三点始终共线,A和B分别在O的两侧.引力常数为G.求两星球做圆周运动的周期.
如图,质量分别为m和M的两个星球A和B在引力作用下都绕O点做匀速圆周运动,星球A和B两者中心之间的距离为L.已知A、B的中心和O三点始终共线,A和B分别在O的两侧.引力常数为G.求两星球做圆周运动的周期.分析:该题属于双星问题,它们之间的万有引力提供向心力,它们两颗星的轨道半径的和等于它们之间的距离.代入公式即可解答.
解答:解:A和B绕O做匀速圆周运动,它们之间的万有引力提供向心力,则A和B的向心力相等.且A和B和O始终共线,说明A和B有相同的角速度和周期.
则有:mω2r=Mω2R
又由已知:r+R=L
解得:R=
L
r=
L
对A根据牛顿第二定律和万有引力定律得:
=m(
)2
L
化简得 T=2π
答:两星球做圆周运动的周期:T=2π
则有:mω2r=Mω2R
又由已知:r+R=L
解得:R=
| m |
| m+M |
r=
| M |
| m+M |
对A根据牛顿第二定律和万有引力定律得:
| GMm |
| L2 |
| 2π |
| T |
| M |
| M+m |
化简得 T=2π
|
答:两星球做圆周运动的周期:T=2π
|
点评:该题属于双星问题,要注意的是它们两颗星的轨道半径的和等于它们之间的距离,不能把它们的距离当成轨道半径.

练习册系列答案
相关题目
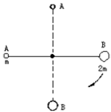 如图,质量分别为m和2m的两个小球A和B,中间用轻质杆相连,在杆的中点O处有一固定转动轴,把杆置于水平位置后释放,在B球顺时针摆动到最低位置的过程中( )
如图,质量分别为m和2m的两个小球A和B,中间用轻质杆相连,在杆的中点O处有一固定转动轴,把杆置于水平位置后释放,在B球顺时针摆动到最低位置的过程中( )| A、杆对球的力沿杆方向 | B、杆对A球做正功,杆对B球做负功 | C、A球、B球、杆和地球组成的系统机械能守恒 | D、重力对A球做功的瞬时功率一直变大 |
 如图,质量分别为m和M的两个星球A和B在引力作用下都绕O点做匀速周运动,星球A和B两者中心之间距离为L.已知A、B的中心和O三点始终共线,A和B分别在O的两侧.引力常数为G.
如图,质量分别为m和M的两个星球A和B在引力作用下都绕O点做匀速周运动,星球A和B两者中心之间距离为L.已知A、B的中心和O三点始终共线,A和B分别在O的两侧.引力常数为G. 如图,质量分别为m和2.5m的两个小球A、B固定在弯成90°角的绝缘轻杆两端,OA和OB的长度均为l,可绕过O点且与纸面垂直的水平轴无摩擦转动,空气阻力不计.设A球带正电,B球带负电,电量均为q,处在竖直向下的匀强电场中,场强大小为E=
如图,质量分别为m和2.5m的两个小球A、B固定在弯成90°角的绝缘轻杆两端,OA和OB的长度均为l,可绕过O点且与纸面垂直的水平轴无摩擦转动,空气阻力不计.设A球带正电,B球带负电,电量均为q,处在竖直向下的匀强电场中,场强大小为E= 如图,质量分别为m和2.5m的两个小球A、B固定在弯成90°角的绝缘轻杆两端,OA和OB的长度均为l,可绕过O点且与纸面垂直的水平轴无摩擦转动,空气阻力不计.设A球带正电,B球带负电,电量均为q,处在竖直向下的匀强电场中,场强大小为E=mg/q.开始时,杆OA水平,由静止释放.求:
如图,质量分别为m和2.5m的两个小球A、B固定在弯成90°角的绝缘轻杆两端,OA和OB的长度均为l,可绕过O点且与纸面垂直的水平轴无摩擦转动,空气阻力不计.设A球带正电,B球带负电,电量均为q,处在竖直向下的匀强电场中,场强大小为E=mg/q.开始时,杆OA水平,由静止释放.求: