题目内容
18. 在真空中有大小为B=1.0T、方向垂直纸面向里的环形匀强磁场,内环半径R1=$\frac{\sqrt{3}}{3}$m,外环半径R2=1.0m.在圆心O与内环间加上电压U后,内圆内形成一个辐射性的电场.荷质比为$\frac{q}{m}$=4.0×103C/kg的带正电的粒子由圆心O处静止释放后经电场加速后进入磁场,不计带电粒子的重力.求
在真空中有大小为B=1.0T、方向垂直纸面向里的环形匀强磁场,内环半径R1=$\frac{\sqrt{3}}{3}$m,外环半径R2=1.0m.在圆心O与内环间加上电压U后,内圆内形成一个辐射性的电场.荷质比为$\frac{q}{m}$=4.0×103C/kg的带正电的粒子由圆心O处静止释放后经电场加速后进入磁场,不计带电粒子的重力.求(1)带电粒子不能穿越磁场外边界的最大电压Um;
(2)当电压为Um时,带电粒子从圆心静止释放后第一次在磁场中的运动时间.
分析 (1)画出粒子的运动轨迹,根据几何关系求出在磁场中做圆周运动的半径,再根据洛伦兹力提供向心力求出最大速度,在加速电场中,根据动能定理求解最大电压;
(2)当所加电压为Um时,从圆心释放的带电粒子经电场、磁场再次回到圆心,画出运动轨迹,根据周期公式结合几何关系求解即可.
解答 解: (1)粒子运动轨迹如图所示,由图知:
(1)粒子运动轨迹如图所示,由图知:
${{R}_{1}}^{2}+{r}^{2}=({R}_{2}-r)^{2}$…①
$r=\frac{1}{3}m$…②
粒子在磁场做圆周运动,则有:$Bq{v}_{m}=m\frac{{{v}_{m}}^{2}}{r}$…③
解得:${v}_{m}=\frac{4}{3}×1{0}^{7}m/s$…④
粒子在电场中加速,则有:$q{U}_{m}=\frac{1}{2}m{{v}_{m}}^{2}$…⑤
解得:${U}_{m}=\frac{2}{9}×1{0}^{3}V$…⑥
(2)当所加电压为Um时,从圆心释放的带电粒子经电场、磁场再次回到圆心的轨迹如图所示.由图知
$tanθ=\frac{{R}_{1}}{r}$…⑦
在磁场中的圆心角为α=2π-2θ…⑧
粒子在磁场中做圆周运动的周期 $T=\frac{2πr}{{v}_{m}}$…⑨
在磁场中运动的时间为t1,则有:${t}_{1}=\frac{α}{2π}T$…⑩
联立⑤~⑧解得:t1=1.05×10-3s
答:(1)带电粒子不能穿越磁场外边界的最大电压Um为$\frac{2}{9}×1{0}^{3}V$;
(2)当电压为Um时,带电粒子从圆心静止释放后第一次在磁场中的运动时间为1.05×10-3s.
点评 考查带电粒子在电磁场中的运动,结合牛顿第二定律与动能定理求解,掌握如何画出运动轨迹图,学会求在磁场中运动的时间,难度适中.

 华东师大版一课一练系列答案
华东师大版一课一练系列答案 质量为1kg的物体A放在倾角为30°的粗糙斜面上,一根劲度系数为200N/m的弹簧一端固定在倾斜顶端,另一端连接物体A,弹簧处于原长,物体恰好静止,现将物体沿斜面向下移动4 cm后由静止释放.地面上斜面始终保持静止.下列说法正确的是( )
质量为1kg的物体A放在倾角为30°的粗糙斜面上,一根劲度系数为200N/m的弹簧一端固定在倾斜顶端,另一端连接物体A,弹簧处于原长,物体恰好静止,现将物体沿斜面向下移动4 cm后由静止释放.地面上斜面始终保持静止.下列说法正确的是( )| A. | 物体受到斜面的静摩擦力大小为3N,方向沿斜面向下 | |
| B. | 物体受到斜面的滑动摩擦力大小为5N,方向沿斜面向下 | |
| C. | 斜面体对地面的压力小于物体与斜面体的总重力 | |
| D. | 斜面体对受到地面对其向左的摩擦力 |
 图中坐标原点处的质点O为一简谐波的波源,当t=0s时,质点O从平衡位置开始振动,波沿x轴向两侧传播,P质点的平衡位置在1m~2m之间,Q质点的平衡位置在2m~3m之间.t1=2s时刻波形第一次如图所示,此时质点P、Q到平衡位置的距离相等,则( )
图中坐标原点处的质点O为一简谐波的波源,当t=0s时,质点O从平衡位置开始振动,波沿x轴向两侧传播,P质点的平衡位置在1m~2m之间,Q质点的平衡位置在2m~3m之间.t1=2s时刻波形第一次如图所示,此时质点P、Q到平衡位置的距离相等,则( )| A. | 波源O的初始振动方向是从平衡位置沿y轴向下 | |
| B. | 从t2=2.5s开始计时,质点P比Q先回到平衡位置 | |
| C. | 当t2=2.5s时,P、Q两质点的位移、加速度相同,速度方向相反 | |
| D. | 当t2=2.5s时,-4m和4m两处的质点分别沿波的传播方向传到-5m和5m的位置 |
| A. | 电场强度为零的地方,电势也为零 | |
| B. | 匀强电场的场强大小处处相等,方向也处处相同 | |
| C. | 带电粒子总是从高电势向低电势运动 | |
| D. | 电场力做正功,带电粒子的电势能可能增大 |
 物理兴趣小组测量一摄像机电池的电动势和内阻.已知该电池电动势约为8V,内阻约1Ω,实验室备有下列器材:
物理兴趣小组测量一摄像机电池的电动势和内阻.已知该电池电动势约为8V,内阻约1Ω,实验室备有下列器材: (量程0.6A,内阻为3Ω)
(量程0.6A,内阻为3Ω) (量程3V,内阻为3kΩ)
(量程3V,内阻为3kΩ) (量程30V,内阻为30kΩ)
(量程30V,内阻为30kΩ)

 如图某位同学设计了一个验证机械能守恒的实验.所用器材有:质量m=0.2kg的小球、压力传感器、半径为1.2m,内径稍大于小球直径的$\frac{3}{4}$圆管.
如图某位同学设计了一个验证机械能守恒的实验.所用器材有:质量m=0.2kg的小球、压力传感器、半径为1.2m,内径稍大于小球直径的$\frac{3}{4}$圆管.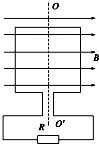 如图所示,匝数为100匝、边长为0.2m的正方形线圈,在磁感应强度为2T的匀强磁场中,从中性面开始以10π rad/s的角速度绕OO′轴匀速转动.若线圈自身电阻为2Ω,负载电阻R=6Ω,取π2=10,则:
如图所示,匝数为100匝、边长为0.2m的正方形线圈,在磁感应强度为2T的匀强磁场中,从中性面开始以10π rad/s的角速度绕OO′轴匀速转动.若线圈自身电阻为2Ω,负载电阻R=6Ω,取π2=10,则: