题目内容
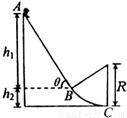
某幼儿园的滑梯如图所示,其中AB段为一倾角为θ的粗糙斜面,BC段为一段半径为R的光滑圆弧,其底端切线沿水平方向.若一儿童自A点由静止滑到C点时,对C点的压力大小为其体重的n倍,已知A与B、B与C间的高度差分别为h1、h2,重力加速度为g,求:(1)儿童经过B点时的速度大小;
(2)儿童与斜面间的动摩擦因数μ.
【答案】分析:(1)儿童从B到C做圆周运动,C点处由牛顿第二定律可求得速度;对B到C过程,由机械能守恒可求得B点的速度;
(2)从A到B的过程中,由动能定理可求得儿童与斜面间的动摩擦因数.
解答:解:(1)儿童对C处的压力大小为F,由牛顿第二定律可知: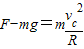
儿童由B至C,由机械能守恒可知: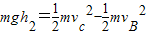
由以上两式可得: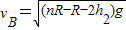
(2)设儿童与斜面间的动摩擦因数μ,儿童所受摩擦力F1=μmgcosθ
儿童由A至B,由动能定律可知: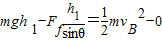
综上可得: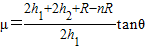
答:(1)儿童经过B点时的速度为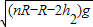 ;(2)儿童与斜面间的动摩擦因数为
;(2)儿童与斜面间的动摩擦因数为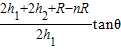 .
.
点评:对于动能定理的应用要明确运动的过程,正确的受力分析,找出合适的规律即可顺利求解.
(2)从A到B的过程中,由动能定理可求得儿童与斜面间的动摩擦因数.
解答:解:(1)儿童对C处的压力大小为F,由牛顿第二定律可知:
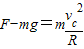
儿童由B至C,由机械能守恒可知:
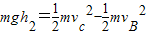
由以上两式可得:
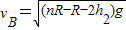
(2)设儿童与斜面间的动摩擦因数μ,儿童所受摩擦力F1=μmgcosθ
儿童由A至B,由动能定律可知:
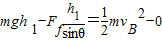
综上可得:
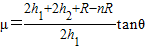
答:(1)儿童经过B点时的速度为
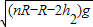 ;(2)儿童与斜面间的动摩擦因数为
;(2)儿童与斜面间的动摩擦因数为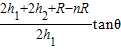 .
.点评:对于动能定理的应用要明确运动的过程,正确的受力分析,找出合适的规律即可顺利求解.

练习册系列答案
相关题目
 某幼儿园的滑梯如图所示,其中AB段为一倾角为θ的粗糙斜面,BC段为一段半径为R的光滑圆弧,其底端切线沿水平方向.若一儿童自A点由静止滑到C点时,对C点的压力大小为其体重的n倍,已知A与B、B与C间的高度差分别为h1、h2,重力加速度为g,求:
某幼儿园的滑梯如图所示,其中AB段为一倾角为θ的粗糙斜面,BC段为一段半径为R的光滑圆弧,其底端切线沿水平方向.若一儿童自A点由静止滑到C点时,对C点的压力大小为其体重的n倍,已知A与B、B与C间的高度差分别为h1、h2,重力加速度为g,求: 的粗糙斜面,BC段为一段半径为R的光滑圆弧,其底端切线沿水平方向.若一儿童自A点由静止滑到C点时,对C点的压力大小为其体重的n倍,已知A与B、B与C间的高度差分别为h1、h2,重力加速度为g,求:
的粗糙斜面,BC段为一段半径为R的光滑圆弧,其底端切线沿水平方向.若一儿童自A点由静止滑到C点时,对C点的压力大小为其体重的n倍,已知A与B、B与C间的高度差分别为h1、h2,重力加速度为g,求:
 .
. 的粗糙斜面,BC段为一段半径为R的光滑圆弧,其底端切线沿水平方向.若一儿童自A点由静止滑到C点时,对C点的压力大小为其体重的n倍,已知A与B、B与C间的高度差分别为h1、h2,重力加速度为g,求:
的粗糙斜面,BC段为一段半径为R的光滑圆弧,其底端切线沿水平方向.若一儿童自A点由静止滑到C点时,对C点的压力大小为其体重的n倍,已知A与B、B与C间的高度差分别为h1、h2,重力加速度为g,求:
 .
. 的粗糙斜面,BC段为一段半径为R的光滑圆弧,其底端切线沿水平方向.若一儿童自A点由静止滑到C点时,对C点的压力大小为其体重的n倍,已知A与B、B与C间的高度差分别为h1、h2,重力加速度为g,求:
的粗糙斜面,BC段为一段半径为R的光滑圆弧,其底端切线沿水平方向.若一儿童自A点由静止滑到C点时,对C点的压力大小为其体重的n倍,已知A与B、B与C间的高度差分别为h1、h2,重力加速度为g,求:
 .
.