Question

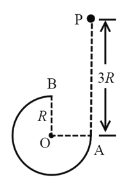
【题目】如图所示，在竖直平面内有一半径为的圆弧轨道，半径水平、竖直，一个质量为的小球自A的正上方P点由静止开始自由下落，小球沿轨道到达最高点B时恰好对轨道没有压力。己知，重力加速度为，则小球从P到B的运动过程中

A.重力做功B.机械能减少

C.合外力做功D.克服摩擦力做功

Answer 1

【答案】D

【解析】

A．重力做功与路径无关，只与初末位置有关，故小球从P到B的运动过程中，重力做功为

WG=mg2R=2mgR

故A错误；

BD．小球沿轨道到达最高点B时恰好对轨道没有压力，根据牛顿第二定律，有

解得：

从P到B过程，重力势能减小量为2mgR，动能增加量为

故机械能减小量为

从P到B过程，克服摩擦力做功等于机械能减小量，故为，故B错误，D正确；

C．从P到B过程，合外力做功等于动能增加量，故

故C错误。