题目内容
10. 如图所示,a、b、c是在地球大气层外圆形轨道上运行的3颗人造卫星,b、c的轨道半径相等,且大于a的轨道半径,下列说法正确的是( )
如图所示,a、b、c是在地球大气层外圆形轨道上运行的3颗人造卫星,b、c的轨道半径相等,且大于a的轨道半径,下列说法正确的是( )| A. | b、c的线速度大小相等,且大于a的线速度 | |
| B. | b、c的向心加速度大小相等,且大于a的向心加速度 | |
| C. | b、c所受向心力大小相等 | |
| D. | a、c所受向心力大小有可能相等 |
分析 根据人造卫星的万有引力等于向心力,列式求出线速度、角速度和向心力的表达式进行讨论即可.
解答 解:人造卫星绕地球做匀速圆周运动,根据万有引力提供向心力,设卫星的质量为m、轨道半径为r、地球质量为M,有
F=F向
F=$\frac{GM}{{r}^{2}}$
F向=m$\frac{{v}^{2}}{r}$=ma═mω2r
解得加速度a=$\frac{GM}{{r}^{2}}$,速度公式v=$\sqrt{\frac{GM}{r}}$,
由图可以知道,ra<rb=rc
A、b、c的线速度大小相等,且小于a的线速度.故A错误;
B、b、c的向心加速度大小相等,且小于a的向心加速度,故B错误;
C、b、c运行半径相同,但不知道质量关系,所以不能判断出向心力的关系,故C错误;
D、a、c的线半径不相同,但由于不知道质量的关系,所以向心力可能相同,故D正确
故选:D
点评 本题关键抓住万有引力提供向心力,熟练运用向心力公式是解决此类问题的关键

练习册系列答案
相关题目
20. 如图所示,平行金属导轨与水平面间的倾角为θ,导轨电阻不计,与阻值为R的定值电阻相连,匀强磁场垂直穿过导轨平面,磁感应强度为B.有一质量为m、长为l的导体棒从ab位置获得平行于斜面的、大小为v的初速度向上运动,最远到达a′b′的位置,滑行的距离为s,导体棒的电阻也为R,与导轨之间的动摩擦因数为μ.则( )
如图所示,平行金属导轨与水平面间的倾角为θ,导轨电阻不计,与阻值为R的定值电阻相连,匀强磁场垂直穿过导轨平面,磁感应强度为B.有一质量为m、长为l的导体棒从ab位置获得平行于斜面的、大小为v的初速度向上运动,最远到达a′b′的位置,滑行的距离为s,导体棒的电阻也为R,与导轨之间的动摩擦因数为μ.则( )
 如图所示,平行金属导轨与水平面间的倾角为θ,导轨电阻不计,与阻值为R的定值电阻相连,匀强磁场垂直穿过导轨平面,磁感应强度为B.有一质量为m、长为l的导体棒从ab位置获得平行于斜面的、大小为v的初速度向上运动,最远到达a′b′的位置,滑行的距离为s,导体棒的电阻也为R,与导轨之间的动摩擦因数为μ.则( )
如图所示,平行金属导轨与水平面间的倾角为θ,导轨电阻不计,与阻值为R的定值电阻相连,匀强磁场垂直穿过导轨平面,磁感应强度为B.有一质量为m、长为l的导体棒从ab位置获得平行于斜面的、大小为v的初速度向上运动,最远到达a′b′的位置,滑行的距离为s,导体棒的电阻也为R,与导轨之间的动摩擦因数为μ.则( )| A. | 上滑过程中导体棒受到的最大安培力为$\frac{{B}^{2}{l}^{2}v}{2R}$ | |
| B. | 上滑过程中电流做功发出的热量为$\frac{1}{2}$mv2-mgssin θ | |
| C. | 上滑过程中导体棒克服安培力做的功为$\frac{1}{2}$mv2 | |
| D. | 上滑过程中导体棒损失的机械能为$\frac{1}{2}$mv2-mgssin θ |
1. 如图所示,甲、乙两车的质量均为M,静置在光滑的水平面上,两车相距为L,乙车上站立着一个质量也为M的人,他通过一条水平轻绳用恒定的水平拉力F拉甲车直到两车相碰,在此过程中( )
如图所示,甲、乙两车的质量均为M,静置在光滑的水平面上,两车相距为L,乙车上站立着一个质量也为M的人,他通过一条水平轻绳用恒定的水平拉力F拉甲车直到两车相碰,在此过程中( )
 如图所示,甲、乙两车的质量均为M,静置在光滑的水平面上,两车相距为L,乙车上站立着一个质量也为M的人,他通过一条水平轻绳用恒定的水平拉力F拉甲车直到两车相碰,在此过程中( )
如图所示,甲、乙两车的质量均为M,静置在光滑的水平面上,两车相距为L,乙车上站立着一个质量也为M的人,他通过一条水平轻绳用恒定的水平拉力F拉甲车直到两车相碰,在此过程中( )| A. | 甲、乙两车运动过程中某时刻瞬时速度之比为1:2 | |
| B. | 甲、乙两车运动的距离之比为2:1 | |
| C. | 人拉绳所做的功为FL | |
| D. | 人拉绳所做的功为$\frac{2}{3}$FL |
18. 在冬季的北方,坐在垫子上从倾斜的冰滑道上向下滑是人们喜欢的娱乐活动,如图是某人从倾斜的冰滑道下滑直至停在水平面上的v-t图象,则( )
在冬季的北方,坐在垫子上从倾斜的冰滑道上向下滑是人们喜欢的娱乐活动,如图是某人从倾斜的冰滑道下滑直至停在水平面上的v-t图象,则( )
 在冬季的北方,坐在垫子上从倾斜的冰滑道上向下滑是人们喜欢的娱乐活动,如图是某人从倾斜的冰滑道下滑直至停在水平面上的v-t图象,则( )
在冬季的北方,坐在垫子上从倾斜的冰滑道上向下滑是人们喜欢的娱乐活动,如图是某人从倾斜的冰滑道下滑直至停在水平面上的v-t图象,则( )| A. | 3s前和3s后的速度方向相反 | B. | 加速运动的加速度大小为4m/s2 | ||
| C. | 6s时的速度大小为6m/s | D. | 运动经过的总路程为144m |
5. 实验观察到,静止在匀强磁场中A点的原子核发生β衰变,衰变产生的新核与β粒子恰在纸面内做匀速圆周运动,粒子的轨迹如图所示,其中粒子在轨迹1是按顺时针方向运动.则( )
实验观察到,静止在匀强磁场中A点的原子核发生β衰变,衰变产生的新核与β粒子恰在纸面内做匀速圆周运动,粒子的轨迹如图所示,其中粒子在轨迹1是按顺时针方向运动.则( )
 实验观察到,静止在匀强磁场中A点的原子核发生β衰变,衰变产生的新核与β粒子恰在纸面内做匀速圆周运动,粒子的轨迹如图所示,其中粒子在轨迹1是按顺时针方向运动.则( )
实验观察到,静止在匀强磁场中A点的原子核发生β衰变,衰变产生的新核与β粒子恰在纸面内做匀速圆周运动,粒子的轨迹如图所示,其中粒子在轨迹1是按顺时针方向运动.则( )| A. | 轨迹1是新核的,粒子在轨迹2是按顺时针方向活动 | |
| B. | 轨迹2是新核的,粒子在轨迹2是按顺时针方向运动 | |
| C. | 轨迹1是新核的,粒子在轨迹2是按逆时针方向运动 | |
| D. | 轨迹2是新核的,粒子在轨迹2是按逆时针方向运动 |
15. 某同学要制作一个简易的温控装置,其原理图如图所示.继电器与热敏电阻R1、滑动变阻器R串联接在电源E两端.当继电器中的电流超过15mA时,衔铁被吸合,加热器停止加热.继电器的电阻为20Ω,热敏电阻的阻值R1与温度t的关系如下表所示:
某同学要制作一个简易的温控装置,其原理图如图所示.继电器与热敏电阻R1、滑动变阻器R串联接在电源E两端.当继电器中的电流超过15mA时,衔铁被吸合,加热器停止加热.继电器的电阻为20Ω,热敏电阻的阻值R1与温度t的关系如下表所示:
(1)提供的实验器材由:电源E(3V,内阻不计)、滑动变阻器R(0~100Ω)、热敏电阻R1、继电器、电阻箱(0~999.9Ω)、开关S、导线若干.
根据上述表格数据可得,该装置控制的温度最低值在30.0℃至40.0℃的范围内(选填“30.0”“40.0”“50.0”…“80.0”),温度最高值在60.0℃至70.0℃的范围内(选填“30.0”“40.0”“50.0”…“80.0”).
(2)欲使衔铁在温度为50℃时被吸合,下列操作步骤正确顺序是⑤①③②④.(填写各步骤前的序号)
①合上开关,调节滑动变阻器的阻值
②断开开关,将电阻箱从电路中移除
③观察到继电器的衔铁被吸合
④将热敏电阻接入电路
⑤断开开关,用电阻箱替换热敏电阻,将阻值调至108.1Ω
 某同学要制作一个简易的温控装置,其原理图如图所示.继电器与热敏电阻R1、滑动变阻器R串联接在电源E两端.当继电器中的电流超过15mA时,衔铁被吸合,加热器停止加热.继电器的电阻为20Ω,热敏电阻的阻值R1与温度t的关系如下表所示:
某同学要制作一个简易的温控装置,其原理图如图所示.继电器与热敏电阻R1、滑动变阻器R串联接在电源E两端.当继电器中的电流超过15mA时,衔铁被吸合,加热器停止加热.继电器的电阻为20Ω,热敏电阻的阻值R1与温度t的关系如下表所示:| t/℃ | 30.0 | 40.0 | 50.0 | 60.0 | 70.0 | 80.0 |
| R1/Ω | 199.5 | 145.4 | 108.1 | 81.8 | 62.9 | 49.1 |
根据上述表格数据可得,该装置控制的温度最低值在30.0℃至40.0℃的范围内(选填“30.0”“40.0”“50.0”…“80.0”),温度最高值在60.0℃至70.0℃的范围内(选填“30.0”“40.0”“50.0”…“80.0”).
(2)欲使衔铁在温度为50℃时被吸合,下列操作步骤正确顺序是⑤①③②④.(填写各步骤前的序号)
①合上开关,调节滑动变阻器的阻值
②断开开关,将电阻箱从电路中移除
③观察到继电器的衔铁被吸合
④将热敏电阻接入电路
⑤断开开关,用电阻箱替换热敏电阻,将阻值调至108.1Ω
19.关于电磁波,下列说法中正确的是( )
| A. | 电磁波是由不均匀变化的电场和磁场产生的 | |
| B. | 电磁波是横波 | |
| C. | 电磁波不能在真空中传播 | |
| D. | 电磁波在不同介质中传播时的速度大小不变 |
 某探究小组为探究向心力与线速度、角速度、圆周半径等大小关系,利用两个相同材质可绕竖直轴转动的水平转盘和两个相同的长方体小橡皮擦进行实验.如图所示,转盘半径分别为2r和r,A点在大转盘的边缘处、B点在大转盘上离转轴距离为r处,C点在小转盘的边缘处,橡皮擦与转盘间的最大静摩擦力是其所受重力的?倍,大转盘通过皮带带动小转盘无打滑地转动.现将一橡皮擦放置在A处,
某探究小组为探究向心力与线速度、角速度、圆周半径等大小关系,利用两个相同材质可绕竖直轴转动的水平转盘和两个相同的长方体小橡皮擦进行实验.如图所示,转盘半径分别为2r和r,A点在大转盘的边缘处、B点在大转盘上离转轴距离为r处,C点在小转盘的边缘处,橡皮擦与转盘间的最大静摩擦力是其所受重力的?倍,大转盘通过皮带带动小转盘无打滑地转动.现将一橡皮擦放置在A处,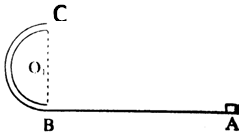 如图所示,半径为R=0.4m的半圆形弯管竖直放置,管的内径远小于弯管的半径且管内光滑,弯管与水平直轨道BA相切于B点,质量为M=0.5kg的物块静止在水平轨道A点,A、B间距离s=2m,物块与水平面间的动摩擦因数μ=0.2,对物块施加一恒力F使其由静止开始从A点加速运动,运动到B点时撤去推力,物块从B点进入半圆轨道,恰能运动到轨道最高点C.(g=10m/s2)问:
如图所示,半径为R=0.4m的半圆形弯管竖直放置,管的内径远小于弯管的半径且管内光滑,弯管与水平直轨道BA相切于B点,质量为M=0.5kg的物块静止在水平轨道A点,A、B间距离s=2m,物块与水平面间的动摩擦因数μ=0.2,对物块施加一恒力F使其由静止开始从A点加速运动,运动到B点时撤去推力,物块从B点进入半圆轨道,恰能运动到轨道最高点C.(g=10m/s2)问: