题目内容
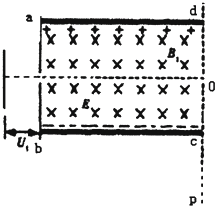 一束质量为m、电荷量为+q的粒子(重力不计),由静止经水平方向的加速电场加速后进入如图所示的正交的匀强电场和匀强磁场区域abcd,电场强度人小为E,磁感应强度人小为B1.粒子直线运动从O点飞出,在cd右侧有一个垂直纸面方向的圆柱形匀强磁场区域.磁应强度大小为B2(图中朱画出).粒子在此磁场作用下,从oc延长线上的p点并与oc延长线成30°夹角射出,op=L,求:
一束质量为m、电荷量为+q的粒子(重力不计),由静止经水平方向的加速电场加速后进入如图所示的正交的匀强电场和匀强磁场区域abcd,电场强度人小为E,磁感应强度人小为B1.粒子直线运动从O点飞出,在cd右侧有一个垂直纸面方向的圆柱形匀强磁场区域.磁应强度大小为B2(图中朱画出).粒子在此磁场作用下,从oc延长线上的p点并与oc延长线成30°夹角射出,op=L,求:(1)加速电压U1;
(2)圆柱形磁场的最小横截面积;
(3)粒子从o点到p点所用时间.
分析:(1)粒子在电场和磁场的复合场中做匀速直线运动,根据平衡得出粒子进入复合场的速度,再根据动能定理求出加速电压的大小.
(2)根据洛伦兹力提供向心力求出粒子在圆形磁场中的运动半径,结合几何关系求出圆柱形磁场的半径,从而得出圆柱形磁场的最小横截面积.
(3)粒子从O到P经历了直线、弧线、又直线运动,结合几何关系求出在磁场外的运行时间,以及根据周期公式求出在磁场中的运行时间,从而得出粒子从O到P的时间.
(2)根据洛伦兹力提供向心力求出粒子在圆形磁场中的运动半径,结合几何关系求出圆柱形磁场的半径,从而得出圆柱形磁场的最小横截面积.
(3)粒子从O到P经历了直线、弧线、又直线运动,结合几何关系求出在磁场外的运行时间,以及根据周期公式求出在磁场中的运行时间,从而得出粒子从O到P的时间.
解答: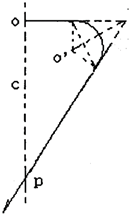 解(1)粒子经加速电场后,速度为v0
解(1)粒子经加速电场后,速度为v0
根据动能定理得,qU1=
mv02
粒子在正交电磁场区域,qE=qv0B1
得到v0=
得U1=
.
(2)带电粒子运动如图,
由qv0B2=m
得R=
圆柱形磁场半径为r=Rcos30°
圆柱形磁场最小横截面为S=πr2=
.
(3)粒子圆周运动周期T=
.
粒子经直线、弧线、又直线运动到p所用时间
t=
+
=
+
-
.
答:(1)加速电压U1=
.
(2)圆柱形磁场的最小横截面积为
.
(3)粒子从o点到p点所用时间
+
-
.
 解(1)粒子经加速电场后,速度为v0
解(1)粒子经加速电场后,速度为v0根据动能定理得,qU1=
| 1 |
| 2 |
粒子在正交电磁场区域,qE=qv0B1
得到v0=
| E |
| B1 |
得U1=
| mE2 |
| 2qB12 |
(2)带电粒子运动如图,
由qv0B2=m
| v02 |
| R |
| mv0 |
| qB2 |
圆柱形磁场半径为r=Rcos30°
圆柱形磁场最小横截面为S=πr2=
| 3πm2E2 |
| 4q2B12B22 |
(3)粒子圆周运动周期T=
| 2πm |
| qB |
粒子经直线、弧线、又直线运动到p所用时间
t=
| ||||
| v0 |
| T |
| 3 |
| ||
| E |
| 2πm |
| 3qB2 |
2
| ||
| qB2 |
答:(1)加速电压U1=
| mE2 |
| 2qB12 |
(2)圆柱形磁场的最小横截面积为
| 3πm2E2 |
| 4q2B12B22 |
(3)粒子从o点到p点所用时间
| ||
| E |
| 2πm |
| 3qB2 |
2
| ||
| qB2 |
点评:解决本题的关键知道粒子经历了加速直线、匀速直线以及在磁场中做匀速圆周运动,结合动能定理、牛顿第二定律和运动学公式进行求解.

练习册系列答案
相关题目
 (2011?石景山区一模)如图所示,圆心在原点、半径为R的圆将xOy平面分为两个区域,在圆内区域Ⅰ(r≤R)和圆外区域Ⅱ(r>R)分别存在两个匀强磁场,方向均垂直于xOy平面.垂直于xOy平面放置两块平面荧光屏,其中荧光屏甲平行于x轴放置在
(2011?石景山区一模)如图所示,圆心在原点、半径为R的圆将xOy平面分为两个区域,在圆内区域Ⅰ(r≤R)和圆外区域Ⅱ(r>R)分别存在两个匀强磁场,方向均垂直于xOy平面.垂直于xOy平面放置两块平面荧光屏,其中荧光屏甲平行于x轴放置在 如图所示,离子发生器发射一束质量为m,电荷量为e,从静止经加速电压U1=5000v加速后,获得速度vo,并沿垂直于电场线方向射入两平行板中央,受偏转电压U2=400v作用后,以速度v离开电场,若两板间距离d=1.0cm,板长l=5.0cm,求:
如图所示,离子发生器发射一束质量为m,电荷量为e,从静止经加速电压U1=5000v加速后,获得速度vo,并沿垂直于电场线方向射入两平行板中央,受偏转电压U2=400v作用后,以速度v离开电场,若两板间距离d=1.0cm,板长l=5.0cm,求: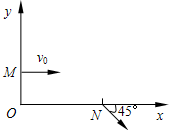 一束质量为m、电荷量为e的电子以速度v0从y轴上的M(0,l0)点以平行于x轴的方向射入存在着沿y轴正向匀强电场的第一象限区域,电子束通过x轴上的N点时与x轴正向成45°角,如图所示.
一束质量为m、电荷量为e的电子以速度v0从y轴上的M(0,l0)点以平行于x轴的方向射入存在着沿y轴正向匀强电场的第一象限区域,电子束通过x轴上的N点时与x轴正向成45°角,如图所示.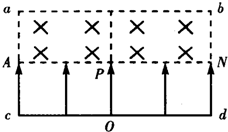 如图所示,一束质量为m、电荷量为q的带正电粒子从O点由静止开始经过匀强电场加速后,均从边界AN的中点P垂直于AN和磁场方向射入磁感应强度为B=
如图所示,一束质量为m、电荷量为q的带正电粒子从O点由静止开始经过匀强电场加速后,均从边界AN的中点P垂直于AN和磁场方向射入磁感应强度为B=