题目内容
已知地球半径R=6400km,地球表面的重力加速度g=10m/s2,不考虑地球自转的影响.求:(1)推导第一宇宙速度v1的表达式,并计算其数值;
(2)若地球自转周期T=24h,计算地球同步卫星距离地面的高度h;
(3)若已知万有引力常量G=6.7×10-11N?m2/kg2,估算地球的平均密度ρ.(以上计算结果保留一位有效数字)
【答案】分析:主要应用在地球表面重力和万有引力相等,卫星运动时万有引力提供圆周运动的向心力,据此列式求解即可.
解答:解:(1)当卫星在地球表面附近运动行时,受地球的万有引力提供向心力,即

得:卫星运行速度 ①
①
又因为在不考虑地球的自转,地球表面的重力和万有引力相等,故有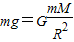 ,所以有
,所以有
GM=gR2 ②
将②代入①可得:
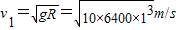 =8×103m/s
=8×103m/s
(2)同步卫星运动地周期与地球自转周期相同,即T=24h=24×3600s,同步卫星受到地球的万有引力提供向心力,故有:
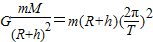
可得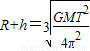 即:
即:
h= ③
③
将②代入③得: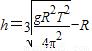 =
= 103m≈4×107m
103m≈4×107m
(3)由②式得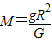 ④
④
由几何知识知,地球的体积V= ⑤
⑤
所以地球的密度ρ=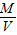 =
=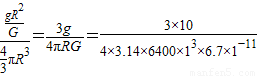 kg/m3≈6×103Kg/m3.
kg/m3≈6×103Kg/m3.
答:(1)第一宇宙速度表达式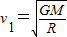 ,数值为8×103m/s;
,数值为8×103m/s;
(2)同步卫星距地面的高度h=4×107m;
(3)地球的平均密度ρ=6×103Kg/m3.
点评:能正确利用万有引力和重力向心力的关系,并能抓住表达式中的变量和不变量进行讨论和计算.
解答:解:(1)当卫星在地球表面附近运动行时,受地球的万有引力提供向心力,即

得:卫星运行速度
 ①
①又因为在不考虑地球的自转,地球表面的重力和万有引力相等,故有
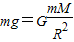 ,所以有
,所以有GM=gR2 ②
将②代入①可得:
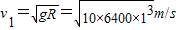 =8×103m/s
=8×103m/s(2)同步卫星运动地周期与地球自转周期相同,即T=24h=24×3600s,同步卫星受到地球的万有引力提供向心力,故有:
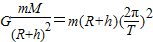
可得
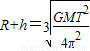 即:
即:h=
 ③
③将②代入③得:
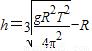 =
= 103m≈4×107m
103m≈4×107m(3)由②式得
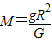 ④
④由几何知识知,地球的体积V=
 ⑤
⑤所以地球的密度ρ=
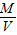 =
=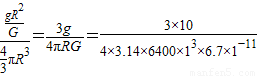 kg/m3≈6×103Kg/m3.
kg/m3≈6×103Kg/m3.答:(1)第一宇宙速度表达式
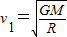 ,数值为8×103m/s;
,数值为8×103m/s;(2)同步卫星距地面的高度h=4×107m;
(3)地球的平均密度ρ=6×103Kg/m3.
点评:能正确利用万有引力和重力向心力的关系,并能抓住表达式中的变量和不变量进行讨论和计算.

练习册系列答案
相关题目
宇航员在地球表面上滑得一单摆的振动周期为2s,若他将这一单摆带到某星球表面上,测得其振动周期为4s,忽略空气阻力,已知该星球的半径与地球半径之比为R星:R地=1:4,设地球表面重力加速度为g,星球表面的重力加速度为g',地球质量为M地,星球质量为M星,则( )
| A、g':g=1:2 | B、g':g=4:1 | C、M星:M地=1:16 | D、M星:M地=1:64 |

