题目内容
6. 质量为m=0.5kg、长L=1m的平板车B静止在光滑水平面上.某时刻质量M=1kg的物体A(视为质点)以v0=4m/s向右的初速度滑上平板车B的上表面,在A滑上B的同时,给B施加一个水平向右的拉力F.已知A与B之间的动摩擦因数μ=0.2,重力加速度g取10m/s2.
质量为m=0.5kg、长L=1m的平板车B静止在光滑水平面上.某时刻质量M=1kg的物体A(视为质点)以v0=4m/s向右的初速度滑上平板车B的上表面,在A滑上B的同时,给B施加一个水平向右的拉力F.已知A与B之间的动摩擦因数μ=0.2,重力加速度g取10m/s2.(1)若F=5N,求从开始到二者共速所需时间,和该时间内A相对B滑行的距离;
(2)若F=5N,在同一坐标系内,定性画出A在B上滑动全程二者的v-t图线(无需计算数值,但必须在图线上标明A、B物体,未标明的不得分);
(3)如果要使A不至于从B上滑落,求拉力F大小应满足的条件.
分析 (1)首先分析物体A和车的运动情况:A相对于地做匀减速运动,车相对于地做匀加速运动.开始阶段,A的速度大于车的速度,则A相对于车向右滑行,当两者速度相等后,A相对于车静止,则当两者速度相等时,物体A在小车上运动时相对小车滑行的最大距离.由牛顿第二定律和运动学公式结合,以及速度相等的条件,分别求出A与车相对于地的位移,两者之差等于A在小车上运动时相对小车滑行的最大距离.
(2)A与B的速度相等后,A受到的摩擦力的方向变成向前,所以A也做加速运动,但小于B的加速度,由此画出v-t图象即可;
(3)要使A不从B上滑落,是指既不能从B的右端滑落,也不能左端滑落.物体A不从右端滑落的临界条件是A到达B的右端时,A、B具有共同的速度,根据牛顿第二定律和运动学公式结合,以及速度相等的条件,可求出此时F,为F的最小值.物体A不从左端滑落的临界条件是A到达B的左端时,A、B具有共同的速度,可求出此时F的最大值,综合得到F的范围.
解答 解:(1)物体A滑上平板车B以后,做匀减速直线运动:μN=MaA
又:N=Mg
得:aA=μg=2 m/s2
平板车B做匀加速直线运动,F+μN=maB
得:aB=14 m/s2
两者速度相同时有:v0-aAt=aBt
解得t=0.25s
对A:${s_A}={v_0}t-\frac{1}{2}{a_A}{t^2}=\frac{15}{16}m$
对B:${s_B}=\frac{1}{2}{a_B}{t^2}=\frac{7}{16}m$
相对运动距离:△s=sA-sB=0.5m
(2)由以上的分析可知,A与B的速度相等前,A做减速运动,B做加速运动;当它们的速度相等后,A的加速度小于B的加速度,所以它们运动的v-t图象如图:
(3)①当F较小时,物体A不滑落的临界条件是A到达B右端时,AB具有共同的速度v,则sA=sB+L,即:
$\frac{{{v_0}+v}}{2}t'=\frac{v}{2}t'+L$
得t'=0.5s
所以:$v={v_0}-{a_A}t'=3m/{s^2}$
代入数据得:${a_B}=\frac{v}{t'}=6m/{s^2}$
又由F1+μMg=maB得F1=1 N
②当F较大时,在A到达B的右端之前,就与B具有相同的速度,之后,A必须相对B静止,否则A会从B的左端滑落,则
对整体:F2=(m+M)a
对物体A:μN=Ma
解得:F2=3 N
综上所述,拉力F大小应满足的条件是1 N≤F≤3 N
答:(1)若F=5N,从开始到二者共速所需时间是0.25s,和该时间内A相对B滑行的距离是0.5m;
(2)定性画出A在B上滑动全程二者的v-t图线如图;
(3)如果要使A不至于从B上滑落,拉力F大小应满足的条件是1 N≤F≤3 N.
点评 牛顿定律和运动公式结合是解决力学问题的基本方法,这类问题的基础是分析物体的受力情况和运动情况,难点在于分析临界状态,挖掘隐含的临界条件.

 寒假学与练系列答案
寒假学与练系列答案 一列波沿直线传播,某一时刻的波形如图所示.质点A的位置与坐标原点O相距0.5m,此时质点A沿y轴正方向运动,再经0.01s第一次达到最大位移处,以下说法正确的是( )
一列波沿直线传播,某一时刻的波形如图所示.质点A的位置与坐标原点O相距0.5m,此时质点A沿y轴正方向运动,再经0.01s第一次达到最大位移处,以下说法正确的是( )| A. | 这列波的波长是2 m | B. | 这列波的频率是50 Hz | ||
| C. | 这列波的波速是50 m/s | D. | 这列波的传播方向为x轴的负方向 |
 如图所示,物块a、b和c的质量之比为1:2:3,a和b、b和c之间用完全相同的轻弹簧S1和S2相连,通过系在a上的细线悬挂于固定点O,整个系统处于静止状态.现将细线剪断,将物块a、b和c的加速度记为a1、a2和a3,S1和S2相对于原长的伸长量分别记为△l1和△l2,重力加速度大小为g,在剪断的瞬间,下列说法正确的是( )
如图所示,物块a、b和c的质量之比为1:2:3,a和b、b和c之间用完全相同的轻弹簧S1和S2相连,通过系在a上的细线悬挂于固定点O,整个系统处于静止状态.现将细线剪断,将物块a、b和c的加速度记为a1、a2和a3,S1和S2相对于原长的伸长量分别记为△l1和△l2,重力加速度大小为g,在剪断的瞬间,下列说法正确的是( )| A. | a1=6g | B. | a2=2.5g | C. | △l1:△l2=5:3 | D. | △l1:△l2=2:3 |
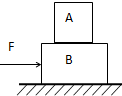 如图所示,木块A质量为1kg,木块B的质量为2kg,叠放在水平地面上,AB间的最大静摩擦力为1N,B与地面间的动摩擦系数为0.1,今用水平力F作用于B,则保持AB相对静止的条件是F不超过( )
如图所示,木块A质量为1kg,木块B的质量为2kg,叠放在水平地面上,AB间的最大静摩擦力为1N,B与地面间的动摩擦系数为0.1,今用水平力F作用于B,则保持AB相对静止的条件是F不超过( )| A. | 1N | B. | 4N | C. | 6N | D. | 8N |
 三角形传送带以1m/s的速度逆时针匀速转动,两边的传送带长都是2m且与水平方向的夹角均为37°.现有两个小物块A、B从传送带底端都以4m/s的初速度冲上传送带,物块与传送带间的动摩擦因数都是0.5,下列说法正确的是( )
三角形传送带以1m/s的速度逆时针匀速转动,两边的传送带长都是2m且与水平方向的夹角均为37°.现有两个小物块A、B从传送带底端都以4m/s的初速度冲上传送带,物块与传送带间的动摩擦因数都是0.5,下列说法正确的是( )| A. | 物块A、B都能到达传送带顶端 | |
| B. | 两物块在传送带上运动的全过程中,物块A、B所受摩擦力一直阻碍物块A、B的运动 | |
| C. | 物块A上冲到与传送带速度相同的过程中,物块相对传送带运动的路程为1.25m | |
| D. | 物块B在上冲过程中在传送带上留下的划痕长度为0.45m |
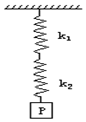 如图所示两个轻质弹簧倔强系数之比为k1:k2=2:1,两弹簧串接后下面悬挂一个重15牛的重物P,平衡后,两弹簧的拉力大小分别为( )
如图所示两个轻质弹簧倔强系数之比为k1:k2=2:1,两弹簧串接后下面悬挂一个重15牛的重物P,平衡后,两弹簧的拉力大小分别为( )| A. | k1和k2的弹力大小均为15牛 | |
| B. | k1和k2的弹力大小均为7.5牛 | |
| C. | k1弹力大小为5牛,k2弹力大小为10牛 | |
| D. | k1弹力大小为10牛,k2弹力大小为5牛 |
| A. | 7 m/s2 | B. | -7 m/s2 | C. | 1 m/s2 | D. | -1 m/s2 |
| A. | 4.1 m/s | B. | 8.2 m/s | C. | 10 m/s | D. | 20 m/s |
