题目内容
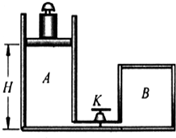
如图所示，截面积为S的气缸A用一个带有阀门K的细管与容器B连通（细管的容积不计）．开始时K关闭，气缸A内充有一定质量的理想气体，B内为真空，气缸A的活塞上放有砝码，此时A内气体温度为T1，活塞静止时与气缸底部的距离为H．打开阀门K后，活塞下降，若将A、B内气体的温度都升高到T2时，活塞仍可升到原来高度H．已知大气压强为 P，活塞与气缸壁之间摩擦可忽略不计，试求：（1）容器B的体积VB；
（2）若再将A和B内相通的气体的温度下降到T1，并将活塞上方的砝码取走，这时活塞又恢复到原来的高度H，若活塞质量为M，则活塞上砝码的质量m为多大？
【答案】分析：（1）气体进入B中的过程是等压变化，根据盖-吕萨克定律列式求解即可；
（2）取走砝码后，活塞又恢复到原来的高度H，根据等温变化列式求解即可．
解答：解：（1）V1=HS，V2=HS+VB，气体进入B中的过程是等压变化，根据盖-吕萨克定律，
因为P1=P2有
=
得VB=
（2）若再将A和B内相通的气体的温度下降到T1，并将活塞上方的砝码取走，
P1=P+
，V1=HS，
V3=HS+VB，P3=P+
，
因为T1=T3，有：P1V1=P3V3
有[P+
]?HS=（P+
）（ HS+VB ）
得：m=
答：（1）容器B的体积是
（2）活塞上砝码的质量是
．
点评：本题关键明确气体的变化特点，然后选择适当的气体状态方程列式求解，不难．
（2）取走砝码后，活塞又恢复到原来的高度H，根据等温变化列式求解即可．
解答：解：（1）V1=HS，V2=HS+VB，气体进入B中的过程是等压变化，根据盖-吕萨克定律，
因为P1=P2有
=得VB=
（2）若再将A和B内相通的气体的温度下降到T1，并将活塞上方的砝码取走，
P1=P+
，V1=HS，V3=HS+VB，P3=P+
，因为T1=T3，有：P1V1=P3V3
有[P+
]?HS=（P+）（ HS+VB ）得：m=
答：（1）容器B的体积是
（2）活塞上砝码的质量是
．点评：本题关键明确气体的变化特点，然后选择适当的气体状态方程列式求解，不难．
练习册系列答案
相关题目
如图所示，截面积为S的气缸A用一个带有阀门K的细管与容器B连通（细管的容积不计）．开始时K关闭，气缸A内充有一定质量的理想气体，B内为真空，气缸A的活塞上放有砝码，此时A内气体温度为T1，活塞静止时与气缸底部的距离为H．打开阀门K后，活塞下降，若将A、B内气体的温度都升高到T2时，活塞仍可升到原来高度H．已知大气压强为 P0，活塞与气缸壁之间摩擦可忽略不计，试求：
如图所示为等离子体发电机原理的示意图，平行金属板间距为d，有足够的长度跟宽度，期间有匀强磁场，磁感应强度为B，方向如图，等离子气流截面积为S，流速为v，等效电阻为r，负载电阻为R，等离子气流从一侧沿着垂直磁场且与极板平行的方向射入极板间．试求：
