题目内容
8. 某同学自制了由两个四分之一的光滑圆弧组成的斜面,两圆弧在O点平滑对接,两圆弧的圆心O1、O2与O点在同一竖直线上,如图所示,已知两圆弧的半径均为R,现将一质量为m的小球从AO弧上某点P由静止释放,已知重力加速度为g.关于小球的运动,下列说法正确的是( )
某同学自制了由两个四分之一的光滑圆弧组成的斜面,两圆弧在O点平滑对接,两圆弧的圆心O1、O2与O点在同一竖直线上,如图所示,已知两圆弧的半径均为R,现将一质量为m的小球从AO弧上某点P由静止释放,已知重力加速度为g.关于小球的运动,下列说法正确的是( )| A. | 当小球从A点释放时,则小球运动到O点时对圆弧的压力为3mg | |
| B. | 当∠PO1O=45°时,则小球运动到O点时恰好做平抛运动 | |
| C. | 当小球运动到O点时恰好做平抛运动,则落地点距O2为$\sqrt{2}$R | |
| D. | 若P点选择合适,可以使得小球沿下圆弧一直运动到B点 |
分析 根据向心力公式和动能定理求出小球到O点时对轨道的压力,在下轨道的最高点$v=\sqrt{gR}$,类似汽车过拱桥最高点,将做平抛运动,根据平抛运动的规律求水平位移,小球在下圆弧轨道上,物块受到重力和支持力,根据牛顿第二定律分析即可求解
解答 解:A、从A→O根据动能定理$mgR=\frac{1}{2}m{v}_{0}^{2}$
${v}_{0}^{\;}=\sqrt{2gR}$
在O点,由向心力公式得${F}_{N}^{\;}-mg=m\frac{{v}_{0}^{2}}{R}$
解得:${F}_{N}^{\;}=3mg$
根据牛顿第三定律小球运动到O点时对圆弧的压力等于圆弧对轨道的压力3mg,故A正确.
B.、当∠PO1O=45°时,根据动能定理,有$mg\frac{R}{2}=\frac{1}{2}m{v}_{0}^{'2}$
${v}_{0}^{'}=\sqrt{gR}$
小球在${O}_{2}^{\;}$圆弧的最高点,有$mg-{F}_{N}^{\;}=m\frac{{v}_{0}^{'2}}{R}$
得${F}_{N}^{\;}=0$
小球在最高点只受重力,做平抛运动,故B正确
C、离开O点做平抛运动,$R=\frac{1}{2}g{t}_{\;}^{2}$
$x={v}_{0}^{′}t$
解得$x=\sqrt{2}R$,故C正确.
D、在下圆弧轨道上,物块只受重力和支持力,运用正交分解法,设物块与圆心连线与竖直方向的夹角为θ,有$mgcosθ-{F}_{N}^{\;}=m\frac{{v}_{\;}^{2}}{R}$,随着θ增加,速度增加,${F}_{N}^{\;}$减小,到某一位置${F}_{N}^{\;}=0$,物块脱离轨道.故D错误
故选:ABC
点评 ABC是常规题,D选项有一定难度.本题的D选项可以证明当从静止开始从下圆弧轨道最高点释放,在距地面$h=\frac{2}{3}R$处时脱离轨道,本题中从上圆弧适当位置释放,到达下圆弧最高点已有速度,比静止时先脱离轨道.

 应用题作业本系列答案
应用题作业本系列答案 如图所示,将一个可视为质点的小球在某一高处沿水平方向抛出,正好垂直打在倾角为θ的斜面上,已知小球在空中飞行的时间为t,重力加速度为g,忽略小球所受空气阻力,下列判断正确的是( )
如图所示,将一个可视为质点的小球在某一高处沿水平方向抛出,正好垂直打在倾角为θ的斜面上,已知小球在空中飞行的时间为t,重力加速度为g,忽略小球所受空气阻力,下列判断正确的是( )| A. | 小球抛出时的速度大小为gtcotθ | |
| B. | 小球刚落到斜面上时的速度大小为$\frac{gt}{tan\;θ}$ | |
| C. | 小球的位移与竖直方向夹角的正切值为2cotθ | |
| D. | 水平分位移与竖直分位移之比为2tanθ |
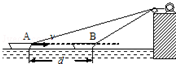 如图,用跨过光滑定滑轮的缆绳将海面上一艘小船直线拖向岸边.已知拖动缆绳的电动机功率恒为P,小船的质量为m,小船所受到水的阻力大小恒为f,经过A点时的速度大小为v,小船从A点沿直线运动到B点经历时间为t,此时缆绳与水平面夹角为θ,A、B两点间水平距离为d,缆绳质量忽略不计.则( )
如图,用跨过光滑定滑轮的缆绳将海面上一艘小船直线拖向岸边.已知拖动缆绳的电动机功率恒为P,小船的质量为m,小船所受到水的阻力大小恒为f,经过A点时的速度大小为v,小船从A点沿直线运动到B点经历时间为t,此时缆绳与水平面夹角为θ,A、B两点间水平距离为d,缆绳质量忽略不计.则( )| A. | 小船经过B点时的速度大小为VB=$\sqrt{{v}^{2}+\frac{2(Pt-fd)}{m}}$ | |
| B. | 小船经过B点时绳子对小船的拉力大小为$\frac{Pcosθ}{\sqrt{{v}^{2}+\frac{2(Pt-fd)}{m}}}$ | |
| C. | 小船经过A点时电动机牵引绳子的速度大小为$\frac{v}{cosθ}$ | |
| D. | 小船经过B点时的加速度大小为$\frac{P}{\sqrt{{m}^{2}{v}^{2}+2m(Pt-fd)}}$-$\frac{f}{m}$ |
| A. | 锌板带正电 | |
| B. | 有正离子从锌板逸出 | |
| C. | 有电子从锌板逸出 | |
| D. | 锌板会吸附空气中的正离子 | |
| E. | 增大紫外线的强度并不能改变光电子的最大初动能 |
 如图,水平转台上有一个质量为m的物块(可视为质点),物块与竖直转轴间距为R,物块与转台间动摩擦因数为μ,且最大静摩擦力等于滑动摩擦力,现让物块始终随转台一起由静止开始缓慢加速转动至角速度为ω时( )
如图,水平转台上有一个质量为m的物块(可视为质点),物块与竖直转轴间距为R,物块与转台间动摩擦因数为μ,且最大静摩擦力等于滑动摩擦力,现让物块始终随转台一起由静止开始缓慢加速转动至角速度为ω时( )| A. | 物块受到的向心力为μmg | B. | 物块受到的摩擦力为mω2R | ||
| C. | 转台对物块做的功为$\frac{1}{2}$mω2R2 | D. | 转台对物块做的功不小于$\frac{1}{2}$μmgR |
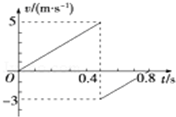 质量为1kg的小球从空中自由下落,与水平地面第一次相碰后反弹到空中某一高度,其速度随时间变化的关系如图所示.若g=10m/s2,则( )
质量为1kg的小球从空中自由下落,与水平地面第一次相碰后反弹到空中某一高度,其速度随时间变化的关系如图所示.若g=10m/s2,则( )| A. | 小球第一次反弹后离开地面的速度的大小为5m/s | |
| B. | 碰撞前后动量改变量的大小为8kg•m/s | |
| C. | 小球是从1.25m高处自由下落的 | |
| D. | 小球反弹起的最大高度为0.45 m |
| A. | 等于在平衡位置时振子的动能 | |
| B. | 等于在最大位移时弹簧的弹性势能 | |
| C. | 等于任意时刻振子动能与弹簧弹性势能之和 | |
| D. | 位移越大振动能量也越大 |
