题目内容
13.假设地球可视为质量均匀分布的球体,其密度为ρ.一颗人造地球卫星在地球上空绕地球做匀速圆周运动,经过时间t,卫星行程为s,卫星与地球中心连线扫过的角度是θ弧度,万有引力常亮为G,求:地球的半径为R=s$\root{3}{\frac{3}{4πGρ{θt}^{2}}}$.分析 根据圆周运动的知识得卫星的线速度与角速度,再根据万有引力提供向心力,表示出地球的质量,结合密度求解地球的半径为R.
解答 解:根据线速度的定义得v=$\frac{s}{t}$
根据角速度的定义得ω=$\frac{θ}{t}$
根据角速度与线速度的关系得r=$\frac{s}{θ}$,
根据万有引力提供向心力
$\frac{GMm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$
M=$\frac{{v}^{2}r}{G}$=ρ•$\frac{4}{3}$πR3
解得R=s$\root{3}{\frac{3}{4πGρ{θt}^{2}}}$
故答案为:s$\root{3}{\frac{3}{4πGρ{θt}^{2}}}$
点评 本题要熟悉线速度的定义和角速度的定义,以及角速度与线速度的关系,这是解决此题的前提.

练习册系列答案
相关题目
3.我国的“嫦娥3号“探月卫星,可贴近月球表面绕圆轨道运行.科学家测得它绕月球的周期为T2,它贴近地球表面绕圆轨道运行的周期为T1,已知万有引力常数为G,仅由以上数据不能求出( )
| A. | 月球的平均密度 | |
| B. | 地球的平均密度 | |
| C. | 月球的平均密度与地球的平均密度的比值 | |
| D. | 月球的质量 |
6. 如图所示,闭合金属铜环从高为h的曲面滚下,沿曲面的另一侧上升,设闭合环初速度为零,不计摩擦,则( )
如图所示,闭合金属铜环从高为h的曲面滚下,沿曲面的另一侧上升,设闭合环初速度为零,不计摩擦,则( )
 如图所示,闭合金属铜环从高为h的曲面滚下,沿曲面的另一侧上升,设闭合环初速度为零,不计摩擦,则( )
如图所示,闭合金属铜环从高为h的曲面滚下,沿曲面的另一侧上升,设闭合环初速度为零,不计摩擦,则( )| A. | 若是匀强磁场,环上升的高度小于h | |
| B. | 若是匀强磁场,环上升的高度大于h | |
| C. | 若是非匀强磁场,环上升的高度等于h | |
| D. | 若是非匀强磁场,环上升的高度小于h |
 某同学设计了一种能自动拐弯的轮子.如图所示,两等高的等距轨道a、b固定于水平桌面上,当装有这种轮子的小车在轨道上运行到达弯道略微偏向轨道外侧时,会顺利实现拐弯而不会出轨.下列截面图所示的轮子中,能实现这一功能的是( )
某同学设计了一种能自动拐弯的轮子.如图所示,两等高的等距轨道a、b固定于水平桌面上,当装有这种轮子的小车在轨道上运行到达弯道略微偏向轨道外侧时,会顺利实现拐弯而不会出轨.下列截面图所示的轮子中,能实现这一功能的是( )



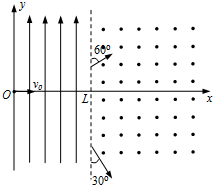 如图所示,在xOy平面内0<x<L的区域内有一方向竖直向上的匀强电场,x>L的区域内有一方向垂直于xOy平面向外的匀强磁场.某时刻,一带正电的粒子从坐标原点,以沿x轴正方向的初速度v0进入电场;之后的另一时刻,一带负电粒子以同样的初速度从坐标原点进入电场.正、负粒子从电场进入磁场时速度方向与电场和磁场边界的夹角分别为60°和30°,两粒子在磁场中分别运动半周后恰好在某点相遇.已知两粒子的重力以及两粒子之间的相互作用都可忽略不计.求:
如图所示,在xOy平面内0<x<L的区域内有一方向竖直向上的匀强电场,x>L的区域内有一方向垂直于xOy平面向外的匀强磁场.某时刻,一带正电的粒子从坐标原点,以沿x轴正方向的初速度v0进入电场;之后的另一时刻,一带负电粒子以同样的初速度从坐标原点进入电场.正、负粒子从电场进入磁场时速度方向与电场和磁场边界的夹角分别为60°和30°,两粒子在磁场中分别运动半周后恰好在某点相遇.已知两粒子的重力以及两粒子之间的相互作用都可忽略不计.求: 如图所示,一木箱静止、在长平板车上,某时刻平板车以a=2.5m/s2的加速度由静止开始向前做匀加速直线运动,当速度达到v=9m/s时改做匀速直线运动,己知木箱与平板车之间的动摩擦因数μ=0.225,箱与平板车之间的最大静摩擦力与滑动静擦力相等(g取10m/s2).求:
如图所示,一木箱静止、在长平板车上,某时刻平板车以a=2.5m/s2的加速度由静止开始向前做匀加速直线运动,当速度达到v=9m/s时改做匀速直线运动,己知木箱与平板车之间的动摩擦因数μ=0.225,箱与平板车之间的最大静摩擦力与滑动静擦力相等(g取10m/s2).求: 如图所示,长为L的细绳一端固定,另一端系一质量为m的小球,给小球一个合适的初速度,小球便可在水平面内做匀速圆周运动,这样就构成了一个圆锥摆,设细绳和竖直方向的夹角为θ,已知当地的重力加速度为g,求:
如图所示,长为L的细绳一端固定,另一端系一质量为m的小球,给小球一个合适的初速度,小球便可在水平面内做匀速圆周运动,这样就构成了一个圆锥摆,设细绳和竖直方向的夹角为θ,已知当地的重力加速度为g,求: 如图所示,一斜面静止在地面上,斜面的倾角为45°,一质量为1kg的物块沿斜面向上滑动,结果地面对斜面的静摩擦力为7N,则斜面与物块间的动摩擦因数为(g=10m/s2)( )
如图所示,一斜面静止在地面上,斜面的倾角为45°,一质量为1kg的物块沿斜面向上滑动,结果地面对斜面的静摩擦力为7N,则斜面与物块间的动摩擦因数为(g=10m/s2)( )


