��Ŀ����
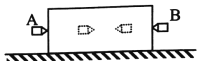
����Ŀ����ͼ��ʾ����ֱ������ϵ�ĵڢ����ֲ��ų�ǿ![]() ������ˮƽ�������ǿ�糡�������������ֲ��Ŵ�ֱֽ���������ǿ�ų�
������ˮƽ�������ǿ�糡�������������ֲ��Ŵ�ֱֽ���������ǿ�ų�![]() �ִӵ糡��
�ִӵ糡��![]() ���ɾ�ֹ�ͷ�һ�Ⱥ�Ϊ
���ɾ�ֹ�ͷ�һ�Ⱥ�Ϊ![]() ���������ƵĴ���������������һ�ν���ų���ֱͨ��x��
���������ƵĴ���������������һ�ν���ų���ֱͨ��x��![]() ��
��

![]() ��ǿ�ų��ĴŸ�Ӧǿ�ȣ�
��ǿ�ų��ĴŸ�Ӧǿ�ȣ�
![]() �������ڶ��ν���ų�ʱ��λ�����ꣻ
�������ڶ��ν���ų�ʱ��λ�����ꣻ
![]() Ϊ��ʹ�����ܻص��ͷŵ�M�������ڶ��ν���ų����ڢ����ĵ糡���������������ͷŵ��ص�M������ʱ�䣮
Ϊ��ʹ�����ܻص��ͷŵ�M�������ڶ��ν���ų����ڢ����ĵ糡���������������ͷŵ��ص�M������ʱ�䣮
���𰸡�![]() 1T
1T ![]()
![]()
��������
������������ǿ�糡����������ƽ���˶�������ƽ���˶����ɣ���ϵ糡ǿ�ȡ���ɵĺ��ʱȣ�������ӵĽ���ų����ٶȴ�С�뷽���Լ�λ��![]() ���������ӽ���ų����������������ã�������Բ���˶�
���������ӽ���ų����������������ã�������Բ���˶�![]() ������һ�ν���ų���ֱͨ��x�ᣬ��Ѱ�ҵ���֪������Բ���뾶�Ĺ�ϵ���Ӷ�����Ÿ�Ӧǿ�ȣ��������ٴν���糡ʱ��������ƽ���˶�
������һ�ν���ų���ֱͨ��x�ᣬ��Ѱ�ҵ���֪������Բ���뾶�Ĺ�ϵ���Ӷ�����Ÿ�Ӧǿ�ȣ��������ٴν���糡ʱ��������ƽ���˶�![]() ������ͬ��������뿪�糡��λ�ã�Ҫ�������ͷŵ��ص�M������ʱ�䣬�����������ӵ��˶��켣������������ƽ���˶�������ƽ���˶��������ʱ�䣬������������Բ���˶�ʱ�������ڹ�ʽ����˶�ʱ�䡣
������ͬ��������뿪�糡��λ�ã�Ҫ�������ͷŵ��ص�M������ʱ�䣬�����������ӵ��˶��켣������������ƽ���˶�������ƽ���˶��������ʱ�䣬������������Բ���˶�ʱ�������ڹ�ʽ����˶�ʱ�䡣
![]() ���ݶ��ܶ����ã�
���ݶ��ܶ����ã�![]()
�������ݽ�ã�![]()
��Ϊ����һ�ν���ų���ֱͨ��x�ᣬ���ݼ��ι�ϵ֪�������ڴų�����Բ���˶��İ뾶![]() ��
��![]() ��
��
���![]() ��
��![]() ���Ӵ�ֱ����糡������ƽ���˶���
���Ӵ�ֱ����糡������ƽ���˶���
��![]() ��
��![]() ��
��
�������ݽ��![]() ��
��
��![]() ��
��
�������ڶ��ν���ų�ʱ��λ������Ϊ![]()
![]() ��һ�ν���ų���켣��ͼ��ʾ:
��һ�ν���ų���켣��ͼ��ʾ:

��ų�ʱ��![]()
![]() ���켣����ͼ��ʾ��
���켣����ͼ��ʾ��![]() ��
��
�������ݵã�![]()

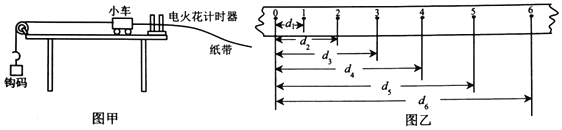
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�