题目内容
17.1969年7月,阿姆斯特朗和另外两名美国宇航员登上月球并进行了一系列的科学实验和生活体验.若他们想在月球上通过小球自由落体实验测出月球的第一宇宙速度,他们必须知道或测出下列哪些物理量( )| A. | 在月球表面高h处释放小球的下落时间 | |
| B. | 小球的质量 | |
| C. | 月球的半径R | |
| D. | 引力常量G |
分析 月球的第一宇宙速度也就是近月卫星的运行速度,根据万有引力提供向心力$G\frac{Mm}{{R}^{2}}=m\frac{{v}^{2}}{R}$,在月球表面的物体受到的重力等于万有引力$mg=G\frac{Mm}{{R}^{2}}$,由此可以计算出月球的第一宇宙速度,再根据自由落体运动的规律计算月球表面的重力加速度.
解答 解:月球的第一宇宙速度也就是近月卫星的运行速度,根据万有引力提供向心力$G\frac{Mm}{{R}^{2}}=m\frac{{v}^{2}}{R}$,得$v=\sqrt{\frac{GM}{R}}$
在月球表面的物体受到的重力等于万有引力$mg=G\frac{Mm}{{R}^{2}}$,得GM=R2g
所以月球的第一宇宙速度为$v=\sqrt{gR}$,其中g为月球表面的重力加速度,R为月球的半径.
若已知在月球表面高h处释放小球的下落时间t,根据自由落体运动的规律$h=\frac{1}{2}g{t}^{2}$,可得$g=\frac{2h}{{t}^{2}}$,
故$v=\sqrt{\frac{2hR}{{t}^{2}}}$,故AC正确、BD错误.
故选:AC.
点评 本题要掌握万有引力提供向心力和重力等于万有引力这两个重要的关系,能够根据自由落体运动的规律计算星球表面的重力加速度.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
20.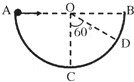 如图所示,在竖直平面内有一个以AB为水平直径的半圆,O为圆心,C为最低点.圆上有一点D,且∠COD=60°.现在A点分别以速率v1、v2沿AB方向先后抛出甲、乙两小球,甲球击中C点,乙球击中D点.重力加速度为g,不计空气阻力.下列说法中正确的是( )
如图所示,在竖直平面内有一个以AB为水平直径的半圆,O为圆心,C为最低点.圆上有一点D,且∠COD=60°.现在A点分别以速率v1、v2沿AB方向先后抛出甲、乙两小球,甲球击中C点,乙球击中D点.重力加速度为g,不计空气阻力.下列说法中正确的是( )
 如图所示,在竖直平面内有一个以AB为水平直径的半圆,O为圆心,C为最低点.圆上有一点D,且∠COD=60°.现在A点分别以速率v1、v2沿AB方向先后抛出甲、乙两小球,甲球击中C点,乙球击中D点.重力加速度为g,不计空气阻力.下列说法中正确的是( )
如图所示,在竖直平面内有一个以AB为水平直径的半圆,O为圆心,C为最低点.圆上有一点D,且∠COD=60°.现在A点分别以速率v1、v2沿AB方向先后抛出甲、乙两小球,甲球击中C点,乙球击中D点.重力加速度为g,不计空气阻力.下列说法中正确的是( )| A. | 圆的半径为R=$\frac{4{{v}_{1}}^{2}}{3g}$ | B. | 圆的半径为R=$\frac{2{{v}_{1}}^{2}}{g}$ | ||
| C. | 甲小球能垂直击中C点 | D. | 乙小球能垂直击中D点 |
12.物体在做曲线运动个过程中,一定变化的物理量是( )
| A. | 加速度 | B. | 速度 | C. | 动能 | D. | 合外力 |
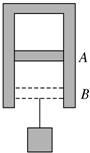 缸内壁光滑且缸壁是导热的.开始活塞静止在离气缸底部h1的A位置,在活塞下端挂上一重物后,活塞经过足够长时间后缓慢下降停在离气缸底部h2的B位置(设周围环境温度保持不变,大气压强为p0,重力加速度为g,活塞面积S),问:在该过程中,缸内气体是吸热还是放热?所挂重物的质量的多少?
缸内壁光滑且缸壁是导热的.开始活塞静止在离气缸底部h1的A位置,在活塞下端挂上一重物后,活塞经过足够长时间后缓慢下降停在离气缸底部h2的B位置(设周围环境温度保持不变,大气压强为p0,重力加速度为g,活塞面积S),问:在该过程中,缸内气体是吸热还是放热?所挂重物的质量的多少? 如图所示,空间的某一区域存在着相互垂直的匀强电场和匀强磁场,一个重力忽略的带电微粒以某一初速度由A点进入这个区域沿直线运动,从C点离开区域;如果将磁场撤去,其他条件不变,则粒子从B点离开场区;如果将电场撤去,其他条件不变,则粒子从D点离开场区.已知BC=CD,设粒子在上述三种情况下,从A到B、从A到C和从A到D所用的时间分别是t1,t2和t3,离开三点时的动能分别是Ek1、Ek2、Ek3,以下关系式正确的是( )
如图所示,空间的某一区域存在着相互垂直的匀强电场和匀强磁场,一个重力忽略的带电微粒以某一初速度由A点进入这个区域沿直线运动,从C点离开区域;如果将磁场撤去,其他条件不变,则粒子从B点离开场区;如果将电场撤去,其他条件不变,则粒子从D点离开场区.已知BC=CD,设粒子在上述三种情况下,从A到B、从A到C和从A到D所用的时间分别是t1,t2和t3,离开三点时的动能分别是Ek1、Ek2、Ek3,以下关系式正确的是( )