题目内容
4.同步卫星与地心的距离为r1,运行速率为v1,向心加速度为a1;近地卫星运行速率为v2,向心加速度为a2,地球半径为r,则下列比值正确的是( )| A. | $\frac{{v}_{1}}{{v}_{2}}$=$\sqrt{\frac{r}{{r}_{1}}}$ | B. | $\frac{{v}_{1}}{{v}_{2}}$=$\frac{{r}_{1}}{r}$ | C. | $\frac{{a}_{1}}{{a}_{2}}$=$\frac{{r}_{1}^{2}}{{r}^{2}}$ | D. | $\frac{{a}_{1}}{{a}_{2}}$=$\frac{{r}^{2}}{{r}_{1}^{2}}$ |
分析 同步卫星运行周期与赤道上物体自转周期相同,根据圆周运动公式比较线速度大小关系,
近地卫星和同步卫星运动时万有引力提供圆周运动的向心力列出表达式比较加速度大小关系.
解答 解:AB、根据万有引力提供向心力$\frac{GMm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$,
解得v=$\sqrt{\frac{GM}{r}}$,
所以$\frac{{v}_{1}}{{v}_{2}}$=$\sqrt{\frac{r}{{r}_{1}}}$,故A正确,B错误;
CD、根据万有引力提供向心力
a=$\frac{GM}{{r}^{2}}$,
则有:$\frac{{a}_{1}}{{a}_{2}}$=$\frac{{r}^{2}}{{r}_{1}^{2}}$,故C错误、D正确;
故选:AD.
点评 万有引力问题的主要处理思路是:环绕天体做圆周运动的向心力由万有引力提供.同时掌握同步卫星的周期与地球自转周期相同是解决本题的关键.

练习册系列答案
相关题目
15. 一小球在外力F的作用下由A运动到B,外力F对小球做功20J,小球克服重力做功10J,克服弹力做功5J,则( )
一小球在外力F的作用下由A运动到B,外力F对小球做功20J,小球克服重力做功10J,克服弹力做功5J,则( )
 一小球在外力F的作用下由A运动到B,外力F对小球做功20J,小球克服重力做功10J,克服弹力做功5J,则( )
一小球在外力F的作用下由A运动到B,外力F对小球做功20J,小球克服重力做功10J,克服弹力做功5J,则( )| A. | 小球在A点的重力势能比B点大10J | |
| B. | 小球在A点的动能比B点小5J | |
| C. | 从A点到B点过程中,小球机械能增加15J | |
| D. | 小球和弹簧组成的系统机械能守恒 |
12.图甲、图乙分别表示两种电压的波形,其中图甲所示电压按正弦规律变化.下列说法正确的是( )
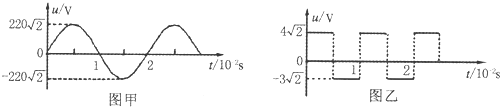
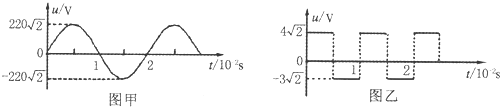
| A. | 图甲表示交流电,图乙表示直流电 | |
| B. | 图乙所示电压的有效值为5V | |
| C. | 将图甲电压通过一个理想二极管给电阻供电,电压的有效值变为110V | |
| D. | 图甲所示电压经匝数比为10:1的变压器变压后,频率变为原来的$\frac{1}{10}$ |
19.在力学理论建立的过程中,有许多伟大的科学家做出了贡献,下列有关科学家和他们的贡献说法正确的是( )
| A. | 卡文迪许通过实验测出了引力常量G | |
| B. | 牛顿用实验直接验证了惯性定律 | |
| C. | 伽利略通过斜面实验合理外推解释了自由落体运动是匀变速直线运动 | |
| D. | 开普勒发现了行星运动的规律 |
16.同一平面内的两个力,大小分别为4N、7N,若两个力同时作用于某一物体,则该物体所受两个力合力可能是( )
| A. | 3N | B. | 10N | C. | 22N | D. | 17N |
3.已知真空中半径为R、电流为I的通电圆线圈轴线上任一点Q的磁感应强度大小为B=$\frac{{μ}_{0}{R}^{2}I}{2\sqrt{({R}^{2}+{x}^{2})^{3}}}$,方向沿轴线,如图甲所示,其中常量μ0为真空磁导率,x为Q点到圆线圈圆心的距离,现真空中有相距为l的两点电荷+q和-q以恒定的角速度ω绕轴OO′(俯视为逆时针)快速转动,如图乙所示,若轴OO′离-q的距离为离+q距离的3倍,则两电荷连线与轴OO′交点P处的磁感应强度( )


| A. | 大小为$\frac{4{μ}_{0}ωq}{3πl}$,方向沿OO′向上 | B. | 大小为$\frac{4{μ}_{0}ωq}{3πl}$,方向沿OO′向下 | ||
| C. | 大小为$\frac{2{μ}_{0}ωq}{3πl}$,方向沿OO′向上 | D. | 大小为$\frac{2{μ}_{0}ωq}{3πl}$,方向沿OO′向下 |
4. 速度相同的一束拉子由左端射入质谱仪后的运动轨迹如图所示,则下列相关说法中正确的是( )
速度相同的一束拉子由左端射入质谱仪后的运动轨迹如图所示,则下列相关说法中正确的是( )
 速度相同的一束拉子由左端射入质谱仪后的运动轨迹如图所示,则下列相关说法中正确的是( )
速度相同的一束拉子由左端射入质谱仪后的运动轨迹如图所示,则下列相关说法中正确的是( )| A. | 该束粒子带负电 | |
| B. | 速度选择器的P1极板带负电 | |
| C. | 能通过狭缝S0的带电粒子的速率等于$\frac{E}{{B}_{1}}$ | |
| D. | 粒子打在胶片上的位置越靠近狭缝S0,粒子的比荷越小 |
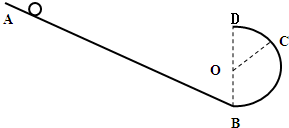 如图所示,竖直平面内的轨道由足够长的光滑斜面轨道AB和半径为R的光滑半圆形轨道BD连接而成,B为半圆形轨道的最低点,D为半圆形轨道的最高点,重力加速度为g,让质量为m的小球从斜面上某点由静止开始释放:
如图所示,竖直平面内的轨道由足够长的光滑斜面轨道AB和半径为R的光滑半圆形轨道BD连接而成,B为半圆形轨道的最低点,D为半圆形轨道的最高点,重力加速度为g,让质量为m的小球从斜面上某点由静止开始释放: 某电视台“快乐向前冲”节目中的场地设施如图所示,AB为水平直轨道,上面安装有电动悬挂器,可以载人运动,水面上漂浮着一个半径为R,加速度为ω,铺有海绵垫的转盘,转盘的轴心离平台的水平距离为L,平台边缘与转盘平面的高度差为H.选手抓住悬挂器,可以在电动机带动下,从A点下方的平台边缘处沿水平方向做初速度为零,加速度为a的匀加速直线运动.选手必须作好判断,在合适的位置放手,才能顺利落在转盘上.设人的质量为m(不计身高大小),人与转盘间的最大静摩擦力为μmg,重力加速度为g.
某电视台“快乐向前冲”节目中的场地设施如图所示,AB为水平直轨道,上面安装有电动悬挂器,可以载人运动,水面上漂浮着一个半径为R,加速度为ω,铺有海绵垫的转盘,转盘的轴心离平台的水平距离为L,平台边缘与转盘平面的高度差为H.选手抓住悬挂器,可以在电动机带动下,从A点下方的平台边缘处沿水平方向做初速度为零,加速度为a的匀加速直线运动.选手必须作好判断,在合适的位置放手,才能顺利落在转盘上.设人的质量为m(不计身高大小),人与转盘间的最大静摩擦力为μmg,重力加速度为g.