题目内容
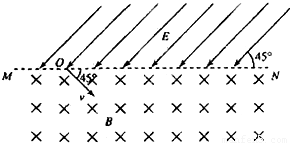
如图,直线MN上方有平行于纸面且与MN成45°的有界匀强电场,电场强度大小未知;MN下方为方向垂直于纸面向里的有界匀强磁场,磁感应强度大小为B.今从MN上的O点向磁场中射入一个速度大小为v、方向与MN成45°角的带正电粒子,该粒子在磁场中运动时的轨道半径为R.该粒子从O点出发记为第一次经过直线MN,第五次经过直线MN时恰好又通过O点.不计粒子的重力.(1)画出粒子在磁场和电场中运动轨迹的草图;
(2)求出电场强度E的大小;
(3)求该粒子再次从O点进入磁场后,运动轨道的半径r;
(4)求该粒子从O点出发到再次回到O点所需的时间t.
【答案】分析:(1)先分析粒子的运动情况再画运动轨迹:粒子先在磁场中做匀速圆周运动,接着逆着电场线进入电场做往复直线运动,再进入磁场做匀速圆周运动,第四次通过MN后进入电场后做类平抛运动,轨迹是抛物线.粒子在磁场中运动速率相等,轨迹半径不变,画出轨迹示意图.
(2)根据几何关系,求出粒子在电场中类平抛运动过程垂直、平行电场方向上的分位移,根据类平抛运动的规律求出电场强度E的大小;
(3)根据牛顿第二定律和运动学公式结合粒子再次从O点进入磁场后的速率,由公式r=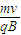 即可求出半径r.
即可求出半径r.
(4)根据粒子运动轨迹对应的圆心角,求出粒子在磁场中的时间;根据牛顿第二定律和运动学公式结合求出电场中运动时间,即可求出总时间.
解答: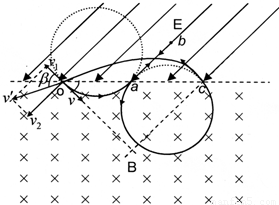 解:(1)粒子的运动轨迹如图.
解:(1)粒子的运动轨迹如图.
(2)由几何关系得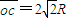 .
.
粒子从c到o做类平抛运动,且在垂直、平行电场方向上的位移相等,都为s⊥=s∥=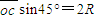
类平抛运动时间为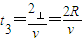
又 s∥=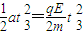
又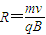
联立得E=vB
(3)粒子在电场中的加速度为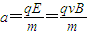
v2=at3=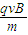 ?
?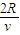 =2v,v1=v
=2v,v1=v
粒子第五次过MN进入磁场后的速度为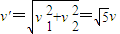
则第五次过MN进入磁场后的圆弧半径为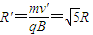
(4)由图知,粒子在磁场中运动的圆心角之和为2π,则粒子在磁场中运动的总时间为等于一个周期,即为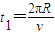
粒子做直线运动所需时间为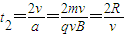
联立得:粒子从出发到第五次到达O点所需时间为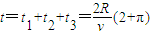
答:(1)画出粒子在磁场和电场中运动轨迹的草图如图;
(2)电场强度E的大小是vB;
(3)该粒子再次从O点进入磁场后,运动轨道的半径是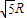 ;
;
(4)求该粒子从O点出发到再次回到O点所需的时间t是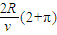 .
.
点评:本题的解题关键是分析粒子的运动情况,画出轨迹,运用运动的分解法研究类平抛运动.
(2)根据几何关系,求出粒子在电场中类平抛运动过程垂直、平行电场方向上的分位移,根据类平抛运动的规律求出电场强度E的大小;
(3)根据牛顿第二定律和运动学公式结合粒子再次从O点进入磁场后的速率,由公式r=
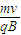 即可求出半径r.
即可求出半径r.(4)根据粒子运动轨迹对应的圆心角,求出粒子在磁场中的时间;根据牛顿第二定律和运动学公式结合求出电场中运动时间,即可求出总时间.
解答:
 解:(1)粒子的运动轨迹如图.
解:(1)粒子的运动轨迹如图.(2)由几何关系得
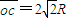 .
.粒子从c到o做类平抛运动,且在垂直、平行电场方向上的位移相等,都为s⊥=s∥=
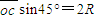
类平抛运动时间为
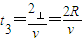
又 s∥=
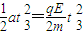
又
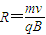
联立得E=vB
(3)粒子在电场中的加速度为
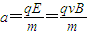
v2=at3=
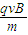 ?
?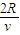 =2v,v1=v
=2v,v1=v粒子第五次过MN进入磁场后的速度为
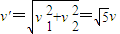
则第五次过MN进入磁场后的圆弧半径为
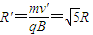
(4)由图知,粒子在磁场中运动的圆心角之和为2π,则粒子在磁场中运动的总时间为等于一个周期,即为
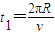
粒子做直线运动所需时间为
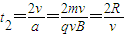
联立得:粒子从出发到第五次到达O点所需时间为
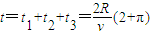
答:(1)画出粒子在磁场和电场中运动轨迹的草图如图;
(2)电场强度E的大小是vB;
(3)该粒子再次从O点进入磁场后,运动轨道的半径是
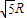 ;
;(4)求该粒子从O点出发到再次回到O点所需的时间t是
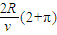 .
.点评:本题的解题关键是分析粒子的运动情况,画出轨迹,运用运动的分解法研究类平抛运动.

练习册系列答案
相关题目
 (2013?重庆一模)如图,直线MN上方有平行于纸面且与MN成45°的有界匀强电场,电场强度大小未知;MN下方为方向垂直于纸面向里的有界匀强磁场,磁感应强度大小为B.今从MN上的O点向磁场中射入一个速度大小为v、方向与MN成45°角的带正电粒子,该粒子在磁场中运动时的轨道半径为R.若该粒子从O点出发记为第一次经过直线MN,而第五次经过直线MN时恰好又通过O点.不计粒子的重力.求:
(2013?重庆一模)如图,直线MN上方有平行于纸面且与MN成45°的有界匀强电场,电场强度大小未知;MN下方为方向垂直于纸面向里的有界匀强磁场,磁感应强度大小为B.今从MN上的O点向磁场中射入一个速度大小为v、方向与MN成45°角的带正电粒子,该粒子在磁场中运动时的轨道半径为R.若该粒子从O点出发记为第一次经过直线MN,而第五次经过直线MN时恰好又通过O点.不计粒子的重力.求: (2011?浙江一模)如图,直线MN上方有平行于纸面且与MN成45°的有界匀强电场,电场强度大小为E;MN下方为方向垂直于纸面向里的有界匀强磁场,磁感应强度大小未知.今从MN上的O点向磁场中射入一个速度大小为v、方向与MN成45°角的带正电粒子,该粒子在磁场中运动时的轨道半径为R.若该粒子从O点进入磁场后第三次经过直线MN后又恰好通过O点.不计粒子的重力.求:
(2011?浙江一模)如图,直线MN上方有平行于纸面且与MN成45°的有界匀强电场,电场强度大小为E;MN下方为方向垂直于纸面向里的有界匀强磁场,磁感应强度大小未知.今从MN上的O点向磁场中射入一个速度大小为v、方向与MN成45°角的带正电粒子,该粒子在磁场中运动时的轨道半径为R.若该粒子从O点进入磁场后第三次经过直线MN后又恰好通过O点.不计粒子的重力.求: 如图,直线MN上方有平行于纸面且与MN成45°的有界匀强电场,电场强度大小未知;MN下方为方向垂直于纸面向里的有界匀强磁场,磁感应强度大小为B.今从MN上的O点向磁场中射入一个速度大小为v、方向与MN成45°角的带正电粒子,该粒子在磁场中运动时的轨道半径为R.该粒子从O点出发记为第一次经过直线MN,第五次经过直线MN时恰好又通过O点.不计粒子的重力.
如图,直线MN上方有平行于纸面且与MN成45°的有界匀强电场,电场强度大小未知;MN下方为方向垂直于纸面向里的有界匀强磁场,磁感应强度大小为B.今从MN上的O点向磁场中射入一个速度大小为v、方向与MN成45°角的带正电粒子,该粒子在磁场中运动时的轨道半径为R.该粒子从O点出发记为第一次经过直线MN,第五次经过直线MN时恰好又通过O点.不计粒子的重力.
 大小未知;MN下方为方向垂直于纸面向里的有界匀强磁场,磁感应强度大小为B。今从MN上的O点向磁场中射入一个速度大小为v、方向与MN成45°角的带正电粒子,该粒子在磁场中运动时的轨道半径为R。若该粒子从O点出发记为第一次经过直线MN,而第五次经过直线MN时恰好又通过O点。不计粒子的重力。求:
大小未知;MN下方为方向垂直于纸面向里的有界匀强磁场,磁感应强度大小为B。今从MN上的O点向磁场中射入一个速度大小为v、方向与MN成45°角的带正电粒子,该粒子在磁场中运动时的轨道半径为R。若该粒子从O点出发记为第一次经过直线MN,而第五次经过直线MN时恰好又通过O点。不计粒子的重力。求: