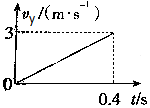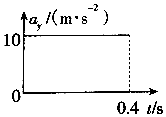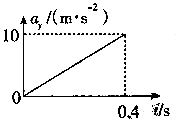题目内容
7.某公共汽车的运行非常规则,先由静止开始匀加速启动,当速度达到v1=10m/s时再做匀速运动,匀速运动的时间t=55s,然后开始匀减速制动,在到达车站时刚好停住.公共汽车在每个车站停车时间均为△t=30s,然后以同样的方式运行至下一站.已知公共汽车在加速启动和减速制动时的加速度大小都为a=2m/s2,而所有相邻车站间的行程都相同.有一次当公共汽车刚刚抵达一个车站时,一辆电动车刚经过该车站一段时间t0=60s,已知该电动车速度大小恒为v2=6m/s,而且行进路线、方向与公共汽车完全相同,不考虑其他交通状况的影响.(1)求两车站间的行程l.
(2)若从下一站开始计数(计为1),公共汽车在刚到达第n站时,电动车也恰好同时到达此车站,则n为多少?
分析 (1)根据速度时间公式求出汽车加速的时间,结合平均速度推论求出加速的位移,由于加速和减速的加速度大小相等,根据运动的对称性得出加速和减速的位移相等,根据位移公式求出匀速运动的位移,从而得出两站间的行程.
(2)根据两车的位移关系,结合运动学的时间关系,运用运动学公式求出n的值.
解答 解:(1)汽车加速时间为:
${t}_{1}=\frac{{v}_{1}}{a}$=$\frac{10}{2}s=5s$,
加速的位移为:
${x}_{1}=\frac{{v}_{1}}{2}{t}_{1}=\frac{10}{2}×5m=25m$,
减速的位移为:
x2=x1=25m,
匀速位移为:
x3=v1t=10×55m=550m.
则两车站间的行程为:l=x1+x2+x3=25+25+550m=600m.
(2)设电动车到第n站用时T,则有:T=n(2t1+t+△t)+t0,
nx=v0T,
代入数据解得:n=12.
答:(1)两车站间的行程为600m.
(2)n为12.
点评 本题主要考查了运动学的基本公式的直接应用,第一问比较简单,理清汽车在整个过程中的运动规律即可求解,对于第二问,关键抓住位移关系和时间关系,运用运动学公式进行求解.

练习册系列答案
相关题目
18.如图,A、B分别为两传动轮边缘上的两点,转动过程中皮带不打滑,A、B两点的( )

| A. | 速率相等 | B. | 线速度相等 | C. | 转速相等 | D. | 角速度相等 |
2. 如图所示,一轻绳绕过无摩擦的两个轻质小定滑轮O1、O2和质量为m的小球连接,另一端与套在光滑直杆上质量也为m的小物块连接,已知直杆两端固定,与两定滑轮在同一竖直平面内,与水平面的夹角θ=60°,直杆上C点与两定滑轮均在同一高度,C点到定滑轮O1的距离为L,杆上D点到C点的距离也是L,重力加速度为g,设直杆足够长,小球运动过程中不会与其他物体相碰.现将小物块从C点由静止释放,则( )
如图所示,一轻绳绕过无摩擦的两个轻质小定滑轮O1、O2和质量为m的小球连接,另一端与套在光滑直杆上质量也为m的小物块连接,已知直杆两端固定,与两定滑轮在同一竖直平面内,与水平面的夹角θ=60°,直杆上C点与两定滑轮均在同一高度,C点到定滑轮O1的距离为L,杆上D点到C点的距离也是L,重力加速度为g,设直杆足够长,小球运动过程中不会与其他物体相碰.现将小物块从C点由静止释放,则( )
 如图所示,一轻绳绕过无摩擦的两个轻质小定滑轮O1、O2和质量为m的小球连接,另一端与套在光滑直杆上质量也为m的小物块连接,已知直杆两端固定,与两定滑轮在同一竖直平面内,与水平面的夹角θ=60°,直杆上C点与两定滑轮均在同一高度,C点到定滑轮O1的距离为L,杆上D点到C点的距离也是L,重力加速度为g,设直杆足够长,小球运动过程中不会与其他物体相碰.现将小物块从C点由静止释放,则( )
如图所示,一轻绳绕过无摩擦的两个轻质小定滑轮O1、O2和质量为m的小球连接,另一端与套在光滑直杆上质量也为m的小物块连接,已知直杆两端固定,与两定滑轮在同一竖直平面内,与水平面的夹角θ=60°,直杆上C点与两定滑轮均在同一高度,C点到定滑轮O1的距离为L,杆上D点到C点的距离也是L,重力加速度为g,设直杆足够长,小球运动过程中不会与其他物体相碰.现将小物块从C点由静止释放,则( )| A. | 当细线与杆垂直时小球正好下降到最低点 | |
| B. | 小球下降距离最大时滑块的加速度5m/s2 | |
| C. | 滑块运动到D点时与小球速度大小相同 | |
| D. | 滑块下降到最低点时下降的竖直高度与小球上升高度相等 |
19.关于电场,下列叙述中正确的是( )
| A. | 以点电荷为圆心,r为半径的球面上,各点的场强都相同 | |
| B. | 正电荷周围的电场强度一定比负电荷周围的电场强度大 | |
| C. | 在电场中某点放入试探电荷q,该点的场强为E=$\frac{F}{q}$,取走q后,该点场强不为零 | |
| D. | 电荷所受电场力越大,该点电场强度一定越大 |
16. 如图所示,重为G的物体在水平向右的压力F作用下静止在竖直墙上,F随时间均匀减小到某值,此过程物体始终静止.设物体与墙的最大静摩擦因数为μ,下列说法正确的是( )
如图所示,重为G的物体在水平向右的压力F作用下静止在竖直墙上,F随时间均匀减小到某值,此过程物体始终静止.设物体与墙的最大静摩擦因数为μ,下列说法正确的是( )
 如图所示,重为G的物体在水平向右的压力F作用下静止在竖直墙上,F随时间均匀减小到某值,此过程物体始终静止.设物体与墙的最大静摩擦因数为μ,下列说法正确的是( )
如图所示,重为G的物体在水平向右的压力F作用下静止在竖直墙上,F随时间均匀减小到某值,此过程物体始终静止.设物体与墙的最大静摩擦因数为μ,下列说法正确的是( )| A. | 墙对物体的弹力随时间均匀减小 | |
| B. | 物体与墙的最大静摩擦力随时间均匀减小 | |
| C. | 物体受到的摩擦力随时间均匀减小 | |
| D. | 物体受到的摩擦力不变,始终等于μG |
17. 如图所示,一铁架台放于水平地面上,其上有一轻质细线悬挂一小球,开始时细线竖直,现将水平力F作用于小球上,使其缓慢地由实线位置运动到虚线位置,铁架台始终保持静止,则在这一过程中( )
如图所示,一铁架台放于水平地面上,其上有一轻质细线悬挂一小球,开始时细线竖直,现将水平力F作用于小球上,使其缓慢地由实线位置运动到虚线位置,铁架台始终保持静止,则在这一过程中( )
 如图所示,一铁架台放于水平地面上,其上有一轻质细线悬挂一小球,开始时细线竖直,现将水平力F作用于小球上,使其缓慢地由实线位置运动到虚线位置,铁架台始终保持静止,则在这一过程中( )
如图所示,一铁架台放于水平地面上,其上有一轻质细线悬挂一小球,开始时细线竖直,现将水平力F作用于小球上,使其缓慢地由实线位置运动到虚线位置,铁架台始终保持静止,则在这一过程中( )| A. | 水平拉力F是恒力 | B. | 铁架台对地面的压力一定不变 | ||
| C. | 细线的拉力变小 | D. | 地面对铁架台的摩擦力增大 |
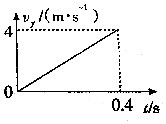
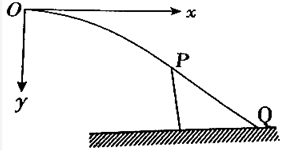 将小球以3m/s的速度水平抛出,它落地速度为5m/s,以vx、vy分别表示水平、竖直分速度,以ay表示竖直分加速度,取g=10m/s2,则图中正确的是( )
将小球以3m/s的速度水平抛出,它落地速度为5m/s,以vx、vy分别表示水平、竖直分速度,以ay表示竖直分加速度,取g=10m/s2,则图中正确的是( )