题目内容
 一直角棱镜的截面为如图所示的Rt△ABC,其顶角α=30°,AB边长为a,光屏PQ与AB平行,距棱镜有一定距离,现有一宽度等于AB的单色光垂直射向AB面,经棱镜折射后在光屏PQ上形成一宽度等于
一直角棱镜的截面为如图所示的Rt△ABC,其顶角α=30°,AB边长为a,光屏PQ与AB平行,距棱镜有一定距离,现有一宽度等于AB的单色光垂直射向AB面,经棱镜折射后在光屏PQ上形成一宽度等于| 2 | 3 |
分析:平行光束垂直射向AB面方向不变,在AC面发生折射,作出光路图.根据几何知识求出AC面上的入射角和折射角,再由折射定律求解折射率n.
解答: 解:作出光路图如图所示,图中表示了经棱镜折射的上、下边缘光线和中间一条代表光线.
解:作出光路图如图所示,图中表示了经棱镜折射的上、下边缘光线和中间一条代表光线.
在Rt△ADE中,由题设条件知,AD边长为
a,因CE长为
a,所以DE长为
a,
则得:tanθ=
=
,
解得:θ=30°
因α=30°,所以β=30°,这样r=90°-β=60°
考虑光线在AC边的折射,由折射定律有:
n=
=
=
答:棱镜的折射率为
.
 解:作出光路图如图所示,图中表示了经棱镜折射的上、下边缘光线和中间一条代表光线.
解:作出光路图如图所示,图中表示了经棱镜折射的上、下边缘光线和中间一条代表光线.在Rt△ADE中,由题设条件知,AD边长为
| ||
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
则得:tanθ=
| ||||
|
| 1 | ||
|
解得:θ=30°
因α=30°,所以β=30°,这样r=90°-β=60°
考虑光线在AC边的折射,由折射定律有:
n=
| sinr |
| sini |
| sin60° |
| sin30° |
| 3 |
答:棱镜的折射率为
| 3 |
点评:本题的解题关键是正确作出光路图,根据几何知识求解入射角和折射角,再运用折射定律求折射率.

练习册系列答案
相关题目

 (2013?湖北模拟)一棱镜的截面为Rt△ABC,∠A=30°,直角边BC=a棱镜材料的折射率为n=
(2013?湖北模拟)一棱镜的截面为Rt△ABC,∠A=30°,直角边BC=a棱镜材料的折射率为n=
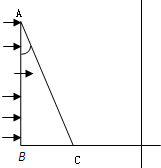 如图所示,△ABC为一直角三棱镜的截面,其顶角α=30°,BC边长为a,棱镜的折射率为
如图所示,△ABC为一直角三棱镜的截面,其顶角α=30°,BC边长为a,棱镜的折射率为