题目内容
一光盘(CD)音轨区域的内半径R1=25mm,外半径R2=58mm,径向音轨密度n=625条/mm.在CD唱机中,光盘每转一圈,激光头沿径向向外移动一条音轨,激光头对光盘以恒定的线速度运动.若开始放音时,光盘的角速度为50rad/s,则全部放完时的角速度是______rad/s;这光盘的总放音时间是______min.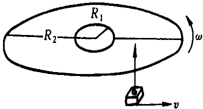

根据R1ω1=R2ω2得,ω2=
=
×50≈21.6rad/s.
光盘转一圈径向过一条音轨,在半径r1处转一圈所用时间为:t1=
.
同理在半径r2,r3,…rn处转一圈所用时间分别为:t2=
=
=t1+
t3=
=
=t2+
…
tn=
显然时间t1,t2,t3…tn为一等差数列.据等差数列求和公式,
取t1=
,tn=
项数n=N(R2-R1)
光盘全部放一遍所用时间为:
t=
≈4300s≈71.7min.
故答案为:21.6,71.7.
| R1ω1 |
| R2 |
| 25 |
| 58 |
光盘转一圈径向过一条音轨,在半径r1处转一圈所用时间为:t1=
| 2πr1 |
| v |
同理在半径r2,r3,…rn处转一圈所用时间分别为:t2=
| 2πr2 |
| v |
| 2π(r1+△r) |
| v |
| 2π△r |
| v |
t3=
| 2πr3 |
| v |
| 2π(r1+2△r) |
| v |
| 2π△r |
| v |
…
tn=
| 2πrn |
| v |
显然时间t1,t2,t3…tn为一等差数列.据等差数列求和公式,
取t1=
| 2πR1 |
| v |
| 2πR2 |
| v |
光盘全部放一遍所用时间为:
t=
| n(t1+tn) |
| 2 |
故答案为:21.6,71.7.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
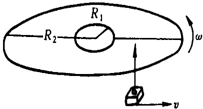 (2005?上海模拟)一光盘(CD)音轨区域的内半径R1=25mm,外半径R2=58mm,径向音轨密度n=625条/mm.在CD唱机中,光盘每转一圈,激光头沿径向向外移动一条音轨,激光头对光盘以恒定的线速度运动.若开始放音时,光盘的角速度为50rad/s,则全部放完时的角速度是
(2005?上海模拟)一光盘(CD)音轨区域的内半径R1=25mm,外半径R2=58mm,径向音轨密度n=625条/mm.在CD唱机中,光盘每转一圈,激光头沿径向向外移动一条音轨,激光头对光盘以恒定的线速度运动.若开始放音时,光盘的角速度为50rad/s,则全部放完时的角速度是 (2011?湖北模拟)一张致密CD光盘音轨区域的内半径为R1=2.2cm,外半径为R2=5.6cm,径向音轨密度为N=650条/mm,在CD唱机内,光盘每转一圈,激光头沿径向向外移动一条音轨,己知每条音轨宽均匀,激光朿相对于光盘以恒定的线速度V=1.3m/s运动.将一张光盘全部播放一遍所用时间是多少?
(2011?湖北模拟)一张致密CD光盘音轨区域的内半径为R1=2.2cm,外半径为R2=5.6cm,径向音轨密度为N=650条/mm,在CD唱机内,光盘每转一圈,激光头沿径向向外移动一条音轨,己知每条音轨宽均匀,激光朿相对于光盘以恒定的线速度V=1.3m/s运动.将一张光盘全部播放一遍所用时间是多少?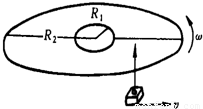 一光盘(CD)音轨区域的内半径R1=25mm,外半径R2=58mm,径向音轨密度n=625条/mm.在CD唱机中,光盘每转一圈,激光头沿径向向外移动一条音轨,激光头对光盘以恒定的线速度运动.若开始放音时,光盘的角速度为50rad/s,则全部放完时的角速度是 rad/s;这光盘的总放音时间是 min.
一光盘(CD)音轨区域的内半径R1=25mm,外半径R2=58mm,径向音轨密度n=625条/mm.在CD唱机中,光盘每转一圈,激光头沿径向向外移动一条音轨,激光头对光盘以恒定的线速度运动.若开始放音时,光盘的角速度为50rad/s,则全部放完时的角速度是 rad/s;这光盘的总放音时间是 min.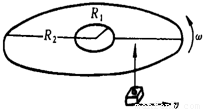 一光盘(CD)音轨区域的内半径R1=25mm,外半径R2=58mm,径向音轨密度n=625条/mm.在CD唱机中,光盘每转一圈,激光头沿径向向外移动一条音轨,激光头对光盘以恒定的线速度运动.若开始放音时,光盘的角速度为50rad/s,则全部放完时的角速度是 rad/s;这光盘的总放音时间是 min.
一光盘(CD)音轨区域的内半径R1=25mm,外半径R2=58mm,径向音轨密度n=625条/mm.在CD唱机中,光盘每转一圈,激光头沿径向向外移动一条音轨,激光头对光盘以恒定的线速度运动.若开始放音时,光盘的角速度为50rad/s,则全部放完时的角速度是 rad/s;这光盘的总放音时间是 min.