题目内容
15. 如图,质量为m1的物体甲通过三段轻绳悬挂,三段轻绳的结点为O,轻绳OB水平且B端与站在水平面上的质量为m2的人相连,轻绳OA与竖直方向的夹角θ=37°,物体甲及人均处于静止状态.已知最大静摩擦力等于滑动摩擦力,sin 37°=0.6,cos 37°=0.8,重力加速度g=10m/s2.
如图,质量为m1的物体甲通过三段轻绳悬挂,三段轻绳的结点为O,轻绳OB水平且B端与站在水平面上的质量为m2的人相连,轻绳OA与竖直方向的夹角θ=37°,物体甲及人均处于静止状态.已知最大静摩擦力等于滑动摩擦力,sin 37°=0.6,cos 37°=0.8,重力加速度g=10m/s2.(1)轻绳OA、OB受到的拉力是多大?
(2)人受到的摩擦力是多大?方向如何?
(3)若人的质量m2=60kg,人与水平面间的动摩擦因数为μ=0.3,则欲使人在水平面上不滑动,物体甲的质量m1最大不能超过多少?
分析 (1)以结点O为研究对象,分析受力,作出力图,根据平衡条件求出轻绳OA、OB受到的拉力.
(2)乙物体水平方向受到OB绳的拉力和水平面的静摩擦力,由二力平衡求解乙受到的摩擦力大小和方向.
(3)当乙物体刚要滑动时,物体甲的质量m1达到最大,此时乙受到的静摩擦力达到最大值Fmax=μm2g,再平衡条件求出物体甲的质量.
解答 解:(1)以结点O为研究对象,如图,由平衡条件有: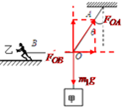
F0B-FOAsinθ=0
F0Acosθ-m1g=0
联立得:
${F_{OA}}=\frac{{{m_1}g}}{cosθ}=\frac{5}{4}{m_1}g$
${F_{OB}}={m_1}gtanθ=\frac{3}{4}{m_1}g$
故轻绳OA、OB受到的拉力分别为$\frac{5}{4}{m_1}g$、$\frac{3}{4}{m_1}g$;
(2)人水平方向受到OB绳的拉力和水平面的静摩擦力,受力如图所示,由平衡条件得: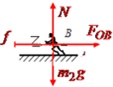
$f={F_{OB}}=\frac{3}{4}{m_1}g$,方向水平向左;
(3)当甲的质量增大到人刚要滑动时,质量达到最大,此时人受到的静摩擦力达到最大值.
当人刚要滑动时,静摩擦力达到最大值fm=μm2g
由平衡条件得:FOBm=fm
又 ${F_{OBm}}={m_{1m}}gtanθ=\frac{3}{4}{m_{1m}}g$
联立得:${m_{1m}}=\frac{{4{F_{OBm}}}}{3g}=\frac{{4μ{m_2}g}}{3g}=24kg$
即物体甲的质量m1最大不能超过24kg.
答:(1)轻绳OA、OB受到的拉力分别为$\frac{5}{4}{m_1}g$、$\frac{3}{4}{m_1}g$;
(2)人受到的摩擦力大小为是$\frac{3}{4}{m_1}g$,方向水平向左;
(3)物体甲的质量m1最大不能超过24kg.
点评 本题涉及共点力平衡中极值问题,当物体刚要滑动时,物体间的静摩擦力达到最大.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案| A. | 做曲线运动的物体,所受合力一定不为零 | |
| B. | 牛顿发现了万有引力定律,并测出了引力常量 | |
| C. | 力是矢量,位移时矢量,所以功也是矢量 | |
| D. | 砸钉子不用橡皮锤,只是因为橡皮锤太轻 |
 在光滑圆锥形容器内固定了一根光滑的竖直细杆,细杆与圆锥的中轴线重合,细杆上穿有小环(小环可以自由转动,但不能上下移动),小环上连接一轻绳,与一质量为m的光猾小球相连,让小球在圆锥内做水平面上的匀速圆周运动,并与圆锥内壁接触.如图所示,图甲中小环与小球在同一水平面上,图乙中轻绳与竖直细杆成θ角.设甲图和乙图中轻绳对球的拉力分别为Ta和Tb,圆锥内壁对小球的支持力分别为Na和Nb,则下列说法中,正确的是( )
在光滑圆锥形容器内固定了一根光滑的竖直细杆,细杆与圆锥的中轴线重合,细杆上穿有小环(小环可以自由转动,但不能上下移动),小环上连接一轻绳,与一质量为m的光猾小球相连,让小球在圆锥内做水平面上的匀速圆周运动,并与圆锥内壁接触.如图所示,图甲中小环与小球在同一水平面上,图乙中轻绳与竖直细杆成θ角.设甲图和乙图中轻绳对球的拉力分别为Ta和Tb,圆锥内壁对小球的支持力分别为Na和Nb,则下列说法中,正确的是( )| A. | Ta一定为零,Tb一定为零 | B. | Ta可以为零,Tb不可以为零 | ||
| C. | Na一定不为零,Nb可以为零 | D. | Na可以为零,Nb可以不为零 |
 如图所示,A、B两物体的质量分别为mA和mB,且mA>mB,整个系统处于静止状态,小滑轮的质量和一切摩擦均不计,如果绳一端由Q点缓慢地向左移动到P点,整个系统重新平衡后,物体A的高度和两滑轮间绳与水平方向的夹角θ如何变化( )
如图所示,A、B两物体的质量分别为mA和mB,且mA>mB,整个系统处于静止状态,小滑轮的质量和一切摩擦均不计,如果绳一端由Q点缓慢地向左移动到P点,整个系统重新平衡后,物体A的高度和两滑轮间绳与水平方向的夹角θ如何变化( )| A. | 物体A的高度升高,θ角不变 | B. | 物体A的高度升高,θ角变大 | ||
| C. | 物体A的高度降低,θ角变小 | D. | 物体A的高度不变,θ角变小 |
 “核反应堆”是通过可控的链式反应实现核能的释放(如图所示),核燃料是铀棒,在铀棒周围要放“慢化剂”,快中子和慢化剂中的碳原子核碰撞后,中子能量减少变为慢中子.碳核的质量是中子的12倍,假设中子与碳核是弹性正碰,而且认为碰撞前中子动能是E0,碳核都是静止的,则( )
“核反应堆”是通过可控的链式反应实现核能的释放(如图所示),核燃料是铀棒,在铀棒周围要放“慢化剂”,快中子和慢化剂中的碳原子核碰撞后,中子能量减少变为慢中子.碳核的质量是中子的12倍,假设中子与碳核是弹性正碰,而且认为碰撞前中子动能是E0,碳核都是静止的,则( )| A. | 链式反应是指由裂变产生的中子使裂变反应一代接一代继续下去的过程 | |
| B. | 镉棒的作用是与铀棒发生化学反应,消耗多余的铀原子核,从而达到控制核反应速度的目的 | |
| C. | 经过一次碰撞,中子失去的动能为$\frac{48}{169}{E_0}$ | |
| D. | 在反应堆的外面修建很厚的水泥防护层是用来屏蔽裂变产物放出的各种射线 |
| A. | 空气阻力对小球做的功为零,重力对小球做的功也为零 | |
| B. | 空气阻力对小球做的功为零,重力对小球做的功为2mgh | |
| C. | 空气阻力对小球做的功为-2fh,重力对小球做的功为零 | |
| D. | 空气阻力对小球做的功为fh,重力对小球做的功为mgh |
| A. | 物体初动能全部转化为热能 | B. | 物体初动能全部转化为势能 | ||
| C. | 物体初动能一部分转化为势能 | D. | 物体初动能全部转化为机械能 |
| A. | 增大入射光的强度,光电流不变 | |
| B. | 减小入射光的强度,光电效应现象可能消失 | |
| C. | 改用频率大于ν的光照射,光电子的最大初动能变大 | |
| D. | 改用频率小于ν的光照射,一定不发生光电效应 |
 如图所示,水平传送带以恒定的速率v运送质量为m的小工件,工件都是在位置A无初速地放到传送带上的,工件与传送带间的动摩擦因数为μ,当前一个工件在传送带上停止相对运动时,后一个工件即放到传送带上.传送带由电动机带动,不计电动机自身和轮轴的能耗.求:
如图所示,水平传送带以恒定的速率v运送质量为m的小工件,工件都是在位置A无初速地放到传送带上的,工件与传送带间的动摩擦因数为μ,当前一个工件在传送带上停止相对运动时,后一个工件即放到传送带上.传送带由电动机带动,不计电动机自身和轮轴的能耗.求: