题目内容
2.以v0的速度水平抛出一物体,当其水平分位移与竖直分位移大小相等时,下列说法错误的是( )| A. | 即时速度的大小是$\sqrt{5}$v0 | |
| B. | 运动时间是$\frac{2{v}_{0}^{\;}}{g}$ | |
| C. | 运动的位移是$\frac{2\sqrt{2}{{v}_{0}}^{2}}{g}$ | |
| D. | 竖直分速度大小等于水平分速度大小 |
分析 物体水平抛出后做平抛运动,根据竖直分位移与水平分位移大小相等,由位移公式列式求出时间.根据时间可求出竖直方向的分速度,再进行合成求解瞬时速度的大小.由位移时间公式求出两个分位移,再进行合成即可求得运动的位移大小.
解答 解:由题意知,平抛运动的水平分位移和竖直分位移大小相等,水平位移$x={v}_{0}^{\;}t$,竖直位移$y=\frac{1}{2}g{t}_{\;}^{2}$,因为x=y,所以${v}_{0}^{\;}t=\frac{1}{2}g{t}_{\;}^{2}$解得t=$\frac{2{v}_{0}^{\;}}{g}$,故B正确
竖直分速度${v}_{y}^{\;}=gt=g×\frac{2{v}_{0}^{\;}}{g}=2{v}_{0}^{\;}$,水平分速度${v}_{x}^{\;}={v}_{0}^{\;}$,所以${v}_{y}^{\;}≠{v}_{x}^{\;}$,故D错误.
即时速度的大小$v=\sqrt{{v}_{0}^{2}+{v}_{y}^{2}}=\sqrt{5}{v}_{0}^{\;}$,故A正确.
水平位移$x={v}_{0}^{\;}t=\frac{2{v}_{0}^{2}}{g}$
竖直位移y=x
运动的合位移$l=\sqrt{{x}_{\;}^{2}+{y}_{\;}^{2}}=\sqrt{2}x=\frac{2\sqrt{2}{v}_{0}^{2}}{g}$,故C正确.
本题选错误的;故选:D
点评 解决本题的关键掌握处理平抛运动的方法:运动的合成与分解,知道平抛运动可分解为水平方向上的匀速直线运动和竖直方向上的自由落体运动,运用运动学的基本规律解题.

练习册系列答案
相关题目
13.一小船渡河,河宽d=150m,水流速度v1=3m/s,船在静水中的速度v2=5m/s,则下列正确的是( )
| A. | 渡河的最短时间为t=30s | |
| B. | 渡河的最小位移为d=150m | |
| C. | 以最小位移过河时,船头与上游河岸之间的夹角为37° | |
| D. | 船不可能垂直到达正对岸 |
10.下列关于静摩擦力的说法中错误的是( )
| A. | 两个相对静止物体间不一定有静摩擦力作用 | |
| B. | 受静摩擦力作用的物体一定是静止的 | |
| C. | 静摩擦力对物体总是阻力 | |
| D. | 静摩擦力一定比滑动摩擦力大 |
17.下列运动的物体,机械能守恒的是( )
| A. | 跳伞运动员在空中匀速下落 | |
| B. | 子弹射穿木块 | |
| C. | 圆锥摆球在水平面内做匀速圆周运动 | |
| D. | 物体沿竖直面内的圆形轨道做匀速圆周运动 |
7. 如图所示,某小组同学利用DIS实验装置研究支架上力的分解.A、B为两个相同的双向力传感器,该型号传感器在受到拉力时读数为正,受到压力时读数为负.A连接质量不计的细绳,可沿固定的板做圆弧形移动.B固定不动,通过光滑铰链连接长0.3m的杆.将细绳连接在杆右端O点构成支架.保持杆在水平方向,按如下步骤操作:
如图所示,某小组同学利用DIS实验装置研究支架上力的分解.A、B为两个相同的双向力传感器,该型号传感器在受到拉力时读数为正,受到压力时读数为负.A连接质量不计的细绳,可沿固定的板做圆弧形移动.B固定不动,通过光滑铰链连接长0.3m的杆.将细绳连接在杆右端O点构成支架.保持杆在水平方向,按如下步骤操作:
①测量绳子与水平杆的夹角∠AOB=θ
②对两个传感器进行调零
③用另一绳在O点悬挂一个钩码,记录两个传感器读数
④取下钩码,移动传感器A改变θ角重复上述实验步骤,得到表格.
根据表格A传感器对应的是表中力F1(选填“F1”或“F2”).钩码质量为0.05kg(保留一位有效数字).
 如图所示,某小组同学利用DIS实验装置研究支架上力的分解.A、B为两个相同的双向力传感器,该型号传感器在受到拉力时读数为正,受到压力时读数为负.A连接质量不计的细绳,可沿固定的板做圆弧形移动.B固定不动,通过光滑铰链连接长0.3m的杆.将细绳连接在杆右端O点构成支架.保持杆在水平方向,按如下步骤操作:
如图所示,某小组同学利用DIS实验装置研究支架上力的分解.A、B为两个相同的双向力传感器,该型号传感器在受到拉力时读数为正,受到压力时读数为负.A连接质量不计的细绳,可沿固定的板做圆弧形移动.B固定不动,通过光滑铰链连接长0.3m的杆.将细绳连接在杆右端O点构成支架.保持杆在水平方向,按如下步骤操作:①测量绳子与水平杆的夹角∠AOB=θ
②对两个传感器进行调零
③用另一绳在O点悬挂一个钩码,记录两个传感器读数
④取下钩码,移动传感器A改变θ角重复上述实验步骤,得到表格.
| F1 | 1.001 | 0.580 | … | 1.002 | … |
| F2 | -0.868 | -0.291 | … | 0.865 | … |
| θ | 30° | 60° | … | 150° | … |
12. 如图所示,地球球心为O,半径为R,表面的重力加速度为g.一宇宙飞船绕地球无动力飞行且沿椭圆轨道运动,轨道上P点距地心最远,距离为3R.为研究方便,假设地球不自转且忽略空气阻力,则( )
如图所示,地球球心为O,半径为R,表面的重力加速度为g.一宇宙飞船绕地球无动力飞行且沿椭圆轨道运动,轨道上P点距地心最远,距离为3R.为研究方便,假设地球不自转且忽略空气阻力,则( )
 如图所示,地球球心为O,半径为R,表面的重力加速度为g.一宇宙飞船绕地球无动力飞行且沿椭圆轨道运动,轨道上P点距地心最远,距离为3R.为研究方便,假设地球不自转且忽略空气阻力,则( )
如图所示,地球球心为O,半径为R,表面的重力加速度为g.一宇宙飞船绕地球无动力飞行且沿椭圆轨道运动,轨道上P点距地心最远,距离为3R.为研究方便,假设地球不自转且忽略空气阻力,则( )| A. | 飞船在P点的加速度一定是$\frac{g}{9}$ | |
| B. | 飞船经过P点的速度一定是 $\sqrt{\frac{gR}{3}}$ | |
| C. | 飞船经过P点的速度小于 $\sqrt{\frac{gR}{3}}$ | |
| D. | 飞船经过P点时,若变轨为半径为3R的圆周运动,需要制动减速 |
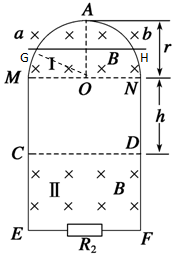 如图所示,竖直平面内有一半径为r、电阻为R1、粗细均匀的光滑半圆形金属环,在M、N处与距离为2r、电阻不计的平行光滑金属导轨ME、NF相接,EF之间接有电阻R2,已知R1=12R,R2=4R.在MN上方及CD下方有水平方向的匀强磁场Ⅰ和Ⅱ,磁感应强度大小均为B.现有质量为m、电阻不计的导体棒ab,从半圆环的最高点A处由静止下落,在下落过程中导体棒始终保持水平,与半圆形金属环及轨道接触良好,设平行导轨足够长.已知导体棒下落r/2时的速度大小为v1,下落到MN处时的速度大小为v2.
如图所示,竖直平面内有一半径为r、电阻为R1、粗细均匀的光滑半圆形金属环,在M、N处与距离为2r、电阻不计的平行光滑金属导轨ME、NF相接,EF之间接有电阻R2,已知R1=12R,R2=4R.在MN上方及CD下方有水平方向的匀强磁场Ⅰ和Ⅱ,磁感应强度大小均为B.现有质量为m、电阻不计的导体棒ab,从半圆环的最高点A处由静止下落,在下落过程中导体棒始终保持水平,与半圆形金属环及轨道接触良好,设平行导轨足够长.已知导体棒下落r/2时的速度大小为v1,下落到MN处时的速度大小为v2.