题目内容
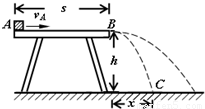
如图所示,小物体放在高度为h=1.25m、长度为S=1.5m的粗糙水平固定桌面的左端A点,以初速度vA=4m/s向右滑行,离开桌子边缘B后,落在水平地面C点,C点与B点的水平距离x=1m,不计空气阻力.试求:(g取10m/s2)(1)小物体离开桌子边缘B时的速度;
(2)小物体与桌面之间的动摩擦因数;
(3)为使小物体离开桌子边缘B后水平射程加倍,则小物体的初速度vA′为多少?
【答案】分析:(1)由平抛运动的规律可求得B点的速度;
(2)由动能定理可求得小物块与桌面间的动摩擦因数;
(3)由平抛运动的规律可求得要使射程加倍时B点的速度,再由动能定理可求得小物块的初速度.
解答:解:(1)小球离开桌面后做平抛运动,竖直方向上有:h= gt2;
gt2;
水平方向上x=vt
联立解得v=2m/s
小物体离开桌子边缘时的速度为2m/s;
(2)物体在桌面上运动时,由动能定理可得:
-μmgs= mv2-
mv2- mvA2;
mvA2;
解得:μ=0.4;
桌面的动摩擦因数为0.4;
(3)要使射程加倍,由平抛运动的规律可知,B点的初速度应加倍,即B点的速度应为2v=4m/s;
则由动能定理可得:
-μmgs= m(2v)2-
m(2v)2- mvA′2
mvA′2
解得:VA′=2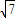 m/s;
m/s;
为使小物体离开桌子边缘B后水平射程加倍,则小物体的初速度为2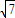 m/s.
m/s.
点评:本题为平抛运动与动能定理结合的题目,要注意正确平抛运动的规律,将平抛运动分解为水平和竖直两个方向进行研究.
(2)由动能定理可求得小物块与桌面间的动摩擦因数;
(3)由平抛运动的规律可求得要使射程加倍时B点的速度,再由动能定理可求得小物块的初速度.
解答:解:(1)小球离开桌面后做平抛运动,竖直方向上有:h=
 gt2;
gt2;水平方向上x=vt
联立解得v=2m/s
小物体离开桌子边缘时的速度为2m/s;
(2)物体在桌面上运动时,由动能定理可得:
-μmgs=
 mv2-
mv2- mvA2;
mvA2; 解得:μ=0.4;
桌面的动摩擦因数为0.4;
(3)要使射程加倍,由平抛运动的规律可知,B点的初速度应加倍,即B点的速度应为2v=4m/s;
则由动能定理可得:
-μmgs=
 m(2v)2-
m(2v)2- mvA′2
mvA′2解得:VA′=2
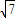 m/s;
m/s;为使小物体离开桌子边缘B后水平射程加倍,则小物体的初速度为2
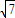 m/s.
m/s.点评:本题为平抛运动与动能定理结合的题目,要注意正确平抛运动的规律,将平抛运动分解为水平和竖直两个方向进行研究.

练习册系列答案
相关题目
 (2011?江苏模拟)如图所示,小物体放在高度为h=1.25m、长度为S=1.5m的粗糙水平固定桌面的左端A点,以初速度vA=4m/s向右滑行,离开桌子边缘B后,落在水平地面C点,C点与B点的水平距离x=1m,不计空气阻力.试求:(g取10m/s2)
(2011?江苏模拟)如图所示,小物体放在高度为h=1.25m、长度为S=1.5m的粗糙水平固定桌面的左端A点,以初速度vA=4m/s向右滑行,离开桌子边缘B后,落在水平地面C点,C点与B点的水平距离x=1m,不计空气阻力.试求:(g取10m/s2) 如图所示,小物体放在高度为h=1.25m、长度为S=1.5m的粗糙水平固定桌面的左端A点,以初速度vA=4m/s向右滑行,离开桌子边缘B后,落在水平地面C点,C点与B点的水平距离x=1m,不计空气阻力.试求:(g取10m/s2)
如图所示,小物体放在高度为h=1.25m、长度为S=1.5m的粗糙水平固定桌面的左端A点,以初速度vA=4m/s向右滑行,离开桌子边缘B后,落在水平地面C点,C点与B点的水平距离x=1m,不计空气阻力.试求:(g取10m/s2) 如图所示,小物体放在高度为h=1.25m、长度为S=1.5m的粗糙水平固定桌面的左端A点,以初速度vA=4m/s向右滑行,离开桌子边缘B后,落在水平地面C点,C点与B点的水平距离x=1m,不计空气阻力.试求:(g取10m/s2)
如图所示,小物体放在高度为h=1.25m、长度为S=1.5m的粗糙水平固定桌面的左端A点,以初速度vA=4m/s向右滑行,离开桌子边缘B后,落在水平地面C点,C点与B点的水平距离x=1m,不计空气阻力.试求:(g取10m/s2)