题目内容
 如图所示,在xoy平面内存在B=2T的匀强磁场,OA与OCA为置于竖直平面内的光滑金属导轨,其中OCA满足曲线方程x=0.5sin
如图所示,在xoy平面内存在B=2T的匀强磁场,OA与OCA为置于竖直平面内的光滑金属导轨,其中OCA满足曲线方程x=0.5sin| π | 5 |
(1)金属棒在导轨上运动时R2上消耗的最大功率;
(2)外力F的最大值.
分析:(1)金属棒沿导轨竖直向上运动,进入磁场中切割磁感线产生感应电动势.当金属棒匀速运动到C点时,电路中感应电动势最大,产生的感应电流最大,根据感应电动势公式Em=Blmv求出感应电动势,由公式P=
求解R2上消耗的最大功率;
(2)金属棒相当于电源,外电路中R1、R2并联,先求出并联阻值.再根据闭合电路欧姆定律求出感应电流的最大值I,最大安培力为 F安=BIxm.即可求解.
| ||
| R2 |
(2)金属棒相当于电源,外电路中R1、R2并联,先求出并联阻值.再根据闭合电路欧姆定律求出感应电流的最大值I,最大安培力为 F安=BIxm.即可求解.
解答:解:(1)金属棒向上匀速运动的过程中切割磁感线,产生电动势,接入电路的有效长度即为OCA导轨形状所满足的曲线方程,因此接入电路的金属棒长度为:
l=x=0.5sin
y
所以当棒运动到C点时,感应电动势最大,即:
Em=Blmv=Bxmv=2×0.5×2V=2V
电阻R1、R2并联,此时R2上消耗的功率最大,最大值为:
P2=
=
W=
W≈0.33W
(2)金属棒相当于电源,外电路中R1、R2并联,其并联阻值为:
R=
=
Ω=4Ω
通过金属棒的最大电流为:
I=
=
A=0.5A
所以最大安培力为:
F安=BIxm=2×0.5×0.5A=0.5N
因为金属棒受力平衡,所以外力的最大值为:
F=F安+mg=0.5N+1N=1.5N
答:(1)金属棒在导轨上运动时R2上消耗的最大功率约为0.33W;
(2)外力F的最大值为1.5N.
l=x=0.5sin
| π |
| 5 |
所以当棒运动到C点时,感应电动势最大,即:
Em=Blmv=Bxmv=2×0.5×2V=2V
电阻R1、R2并联,此时R2上消耗的功率最大,最大值为:
P2=
| ||
| R2 |
| 22 |
| 12 |
| 1 |
| 3 |
(2)金属棒相当于电源,外电路中R1、R2并联,其并联阻值为:
R=
| R1R2 |
| R1+R2 |
| 6×12 |
| 6+12 |
通过金属棒的最大电流为:
I=
| Em |
| R |
| 2 |
| 4 |
所以最大安培力为:
F安=BIxm=2×0.5×0.5A=0.5N
因为金属棒受力平衡,所以外力的最大值为:
F=F安+mg=0.5N+1N=1.5N
答:(1)金属棒在导轨上运动时R2上消耗的最大功率约为0.33W;
(2)外力F的最大值为1.5N.
点评:本题金属棒产生的是正弦式交变电流,解得本题关键要能分析出什么时候感应电动势最大,知道哪部分是电源,哪部分是外电路,知道电路的连接关系.难度中等.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 (2013?安徽模拟)如图所示,在xoy平面上,直线OM与x轴正方向夹角为45°,直线OM左侧存在平行y轴的匀强电场,方向沿y轴负方向.直线OM右侧存在垂直xoy平面向里的磁感应强度为B的匀强磁场.一带电量为q质量为m带正电的粒子(忽略重力)从原点O沿x轴正方向以速度vo射入磁场.此后,粒子穿过磁场与电场的边界三次,恰好从电场中回到原点O.(粒子通过边界时,其运动不受边界的影响)试求:
(2013?安徽模拟)如图所示,在xoy平面上,直线OM与x轴正方向夹角为45°,直线OM左侧存在平行y轴的匀强电场,方向沿y轴负方向.直线OM右侧存在垂直xoy平面向里的磁感应强度为B的匀强磁场.一带电量为q质量为m带正电的粒子(忽略重力)从原点O沿x轴正方向以速度vo射入磁场.此后,粒子穿过磁场与电场的边界三次,恰好从电场中回到原点O.(粒子通过边界时,其运动不受边界的影响)试求: 如图所示,在xOy平面的y轴左侧存在沿y轴正方向的匀强电场,y轴右侧区域Ⅰ内存在磁感应强度大小B1=
如图所示,在xOy平面的y轴左侧存在沿y轴正方向的匀强电场,y轴右侧区域Ⅰ内存在磁感应强度大小B1= (2006?连云港二模)如图所示,在xoy平面上,一个以原点O为中心、半径为R的圆形区域内存在着一匀强磁场.磁场的磁感应强度为B,方向垂直于xoy平面向里.在O点处原来静止着一个具有放射性的原子核--氮(
(2006?连云港二模)如图所示,在xoy平面上,一个以原点O为中心、半径为R的圆形区域内存在着一匀强磁场.磁场的磁感应强度为B,方向垂直于xoy平面向里.在O点处原来静止着一个具有放射性的原子核--氮( 如图所示,在xOy平面上,一个以原点O为圆心,半径为4R的原型磁场区域内存在着匀强磁场,磁场的方向垂直于纸面向里,在坐标(-2R,0)的A处静止着一个具有放射性的原子核氮713N.某时刻该核发生衰变,放出一个正电子和一个反冲核,已知正电子从A处射出时速度方向垂直于x轴,且后来通过了y轴,而反冲核刚好不离开磁场区域.不计重力影响和离子间的相互作用.
如图所示,在xOy平面上,一个以原点O为圆心,半径为4R的原型磁场区域内存在着匀强磁场,磁场的方向垂直于纸面向里,在坐标(-2R,0)的A处静止着一个具有放射性的原子核氮713N.某时刻该核发生衰变,放出一个正电子和一个反冲核,已知正电子从A处射出时速度方向垂直于x轴,且后来通过了y轴,而反冲核刚好不离开磁场区域.不计重力影响和离子间的相互作用.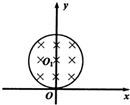 如图所示,在xOy平面上,以y轴上点Ol为圆心,半径为R=0.3m的圆形区域内,分布着一个方向垂直于xOy平面向里,磁感应强度大小为B=0.5T的匀强磁场.一个比荷
如图所示,在xOy平面上,以y轴上点Ol为圆心,半径为R=0.3m的圆形区域内,分布着一个方向垂直于xOy平面向里,磁感应强度大小为B=0.5T的匀强磁场.一个比荷