题目内容
 如图,质量M=3.0kg的小车静止在光滑的水平面上,AD部分是表面粗糙的水平导轨,DC部分是光滑的1/4圆弧形导轨.整个导轨是由绝缘材料制成并处于B=1.0T垂直纸面向里的匀强磁场中.今有一质量m=1.0kg的金属块(可视为质点),带q=2.0×10-3C的负电,以v0=8m/s的速度冲上小车,当将要过D点时,对水平导轨的压力为9.81N(g取9.8m/s2)
如图,质量M=3.0kg的小车静止在光滑的水平面上,AD部分是表面粗糙的水平导轨,DC部分是光滑的1/4圆弧形导轨.整个导轨是由绝缘材料制成并处于B=1.0T垂直纸面向里的匀强磁场中.今有一质量m=1.0kg的金属块(可视为质点),带q=2.0×10-3C的负电,以v0=8m/s的速度冲上小车,当将要过D点时,对水平导轨的压力为9.81N(g取9.8m/s2)(1)求m从A到D过程中,系统的机械能损失多少?
(2)若m通过D点立即撤去磁场,这以后小车能获得的最大速度是多少?
分析:(1)根据共点力平衡求出物体在D点的速度,从而根据水平方向上M和m组成的系统动量守恒求出M的速度,结合能量守恒定律求出系统损失的机械能.
(2)当m返回到D点时,小车的速度最大,根据水平方向上动量守恒、能量守恒求出小车的最大速度.
(2)当m返回到D点时,小车的速度最大,根据水平方向上动量守恒、能量守恒求出小车的最大速度.
解答:解:(1)m将要过D点时,受重力、支持力和洛伦兹力作用,根据共点力平衡得,
N=mg+qvB
解得v=
=
m/s=5m/s.
根据水平方向上系统动量守恒有:
mv0=mv+Mv′
解得v′=
=
m/s=1m/s
根据能量守恒定律得,系统损失的机械能△E=
mv02-
mv2-
Mv′2=
×1×64-
×1×25-
×3×1J=18J.
(2)当m返回到D点时,小车的速度最大,
根据动量守恒定律得,Mv′+mv=mv1+Mv2
根据能量守恒定律有:
Mv′2+
mv2=
mv12+
Mv22
代入数据解得:v2=3m/s,v1=-1m/s.
答:(1)m从A到D过程中,系统的机械能损失为18J.
(2)小车能获得的最大速度是3m/s.
N=mg+qvB
解得v=
| N-mg |
| qB |
| 9.81-9.8 |
| 2×10-3×1 |
根据水平方向上系统动量守恒有:
mv0=mv+Mv′
解得v′=
| mv0-mv |
| M |
| 1×(8-5) |
| 3 |
根据能量守恒定律得,系统损失的机械能△E=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)当m返回到D点时,小车的速度最大,
根据动量守恒定律得,Mv′+mv=mv1+Mv2
根据能量守恒定律有:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
代入数据解得:v2=3m/s,v1=-1m/s.
答:(1)m从A到D过程中,系统的机械能损失为18J.
(2)小车能获得的最大速度是3m/s.
点评:本题是系统动量守恒和能量守恒的类型,寻找解题规律是关键.容易出错的地方,是不认真分析滑块运动过程,认为滑块刚到达D时车的速度就最大.

练习册系列答案
相关题目
 (2013?商丘二模)如图,质量m=2.0kg的物体在水平外力的作用下在水平面上运动,物体和水平面间的动摩擦因数μ=0.05,已知物体运动过程中的坐标与时间的关系为
(2013?商丘二模)如图,质量m=2.0kg的物体在水平外力的作用下在水平面上运动,物体和水平面间的动摩擦因数μ=0.05,已知物体运动过程中的坐标与时间的关系为 如图所示,两块平行金属板MN、PQ竖直放置,两板间的电势差U=1.6×103 V,现将一质量m=3.0×10-2 kg、电荷量q=+4.0×10-5 C的带电小球从两板左上方的A点以初速度v0=4.0m/s水平抛出,已知A点距两板上端的高度h=0.45m,之后小球恰好从MN板上端内侧M点进入两板间匀强电场,然后沿直线运动到PQ板上的C点,不计空气阻力,取g=10m/s2,求:
如图所示,两块平行金属板MN、PQ竖直放置,两板间的电势差U=1.6×103 V,现将一质量m=3.0×10-2 kg、电荷量q=+4.0×10-5 C的带电小球从两板左上方的A点以初速度v0=4.0m/s水平抛出,已知A点距两板上端的高度h=0.45m,之后小球恰好从MN板上端内侧M点进入两板间匀强电场,然后沿直线运动到PQ板上的C点,不计空气阻力,取g=10m/s2,求: 如图,质量M=8kg的小车停放在光滑水平面上,在小车右端施加一水平恒力F=8N.当小车向右运动速度达到3m/s时,在小车的右端轻放一质量m=2kg的小物块,物块与小车间的动摩擦因数μ=0.2,假定小车足够长,试求:
如图,质量M=8kg的小车停放在光滑水平面上,在小车右端施加一水平恒力F=8N.当小车向右运动速度达到3m/s时,在小车的右端轻放一质量m=2kg的小物块,物块与小车间的动摩擦因数μ=0.2,假定小车足够长,试求: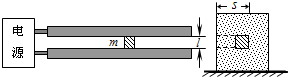 如图,竖直面内两根光滑平行金属导轨沿水平方向固定,其间安放金属滑块,滑块始终与导轨保持良好接触.电源提供的强电流经导轨、滑块、另一导轨流回电源.同时电流在两导轨之间形成较强的磁场(可近似看成匀强磁场),方向垂直于纸面,其强度与电流的大小关系为B=kI,比例常数k=2.5×10-6T/A.已知两导轨内侧间距l=1.5cm,滑块的质量m=3.0×10-2kg,滑块由静止开始沿导轨滑行S=5m后获得的发射速度v=3.0×103m/s(此过程可视为匀加速运动).求:
如图,竖直面内两根光滑平行金属导轨沿水平方向固定,其间安放金属滑块,滑块始终与导轨保持良好接触.电源提供的强电流经导轨、滑块、另一导轨流回电源.同时电流在两导轨之间形成较强的磁场(可近似看成匀强磁场),方向垂直于纸面,其强度与电流的大小关系为B=kI,比例常数k=2.5×10-6T/A.已知两导轨内侧间距l=1.5cm,滑块的质量m=3.0×10-2kg,滑块由静止开始沿导轨滑行S=5m后获得的发射速度v=3.0×103m/s(此过程可视为匀加速运动).求: