题目内容
半径为r=0.5m的圆形空间内，存在垂直于纸面向里地匀强磁场，一带点粒子（不计重力）质量m=1×10-6kg，带电量q=5×10-5C，从A点沿半径方向以速度v=5m/s垂直磁场方向射入磁场中，并从B点射出，∠AOB=90度，如图所示，求：（1）磁感应强度的大小
（2）粒子在磁场中运动的时间．
【答案】分析：（1）根据洛伦兹力提供向心力，由牛顿第二定律列出半径的表达式，从而即可求解；
（2）根据牛顿第二定律，列出周期公式，再由圆心角，即可求解．
解答：
解：确定轨迹的圆心O1，设轨迹半径为R，由几何
关系可求得R=r=0.5m
（1）由R=
可得：
B=
=0.2T
（2）t=
=
=0.628s
答：（1）磁感应强度的大小为0.2T；
（2）粒子在磁场中运动的时间0.628s．
点评：考查洛伦兹作用下做匀速圆周运动，掌握运动轨迹的半径与周期公式，注意几何关系的应用，及圆心角的求法．
（2）根据牛顿第二定律，列出周期公式，再由圆心角，即可求解．
解答：
解：确定轨迹的圆心O1，设轨迹半径为R，由几何关系可求得R=r=0.5m
（1）由R=
可得：B=
=0.2T（2）t=
==0.628s答：（1）磁感应强度的大小为0.2T；
（2）粒子在磁场中运动的时间0.628s．
点评：考查洛伦兹作用下做匀速圆周运动，掌握运动轨迹的半径与周期公式，注意几何关系的应用，及圆心角的求法．
练习册系列答案
相关题目
在光滑的水平面上，一质量为mA=0.1kg的小球A，以8m/s的初速度向右运动，与质量为mB=0.2kg的静止小球B发生弹性正碰．碰后小球B滑向与水平面相切、半径为R=0.5m的竖直放置的光滑半圆形轨道，且恰好能通过最高点N后水平抛出．g=10m/s2．求：
如图所示，一水平放置的半径为r=0.5m的薄圆盘绕过圆心O点的竖直轴转动，圆盘边缘有一质量m=1.0kg的小滑块（可看成是质点）．当圆盘转动的角速度达到某一数值时，滑块从圆盘边缘滑落，滑块与圆盘间的动摩擦因数μ=0.2，圆盘所水平面离水平地面的高度h=2.5m，g取10m/s2．
如图所示，光滑水平面的右端竖直平面内固定一半径为R=0.5m 的光滑半圆槽．质量均为m=1kg的A、B两小球之间有一轻质弹簧，弹簧处于压缩锁定状态．现给A、B一水平向右的初速度v1=2m/s到圆弧最低点M时，弹簧锁定瞬间解除后，小球B恰好能运动到圆弧最高点．求：（ 取g=10m/s2）的速度；
如图所示，粗糙水平地面与半径为R=0.5m的光滑半圆轨道BCD相连接，且在同一竖直平面内，O是BCD的圆心，BOD在同一竖直线上．质量为m=1kg的小物块在水平恒力F=15N的作用下，由静止开始从A点开始做匀加速直线运动，当小物块运动到B点时撤去F，小物块沿半圆轨道运动恰好能通过D点，已知AB间的距离为3m，重力加速度g=10m/s2．求：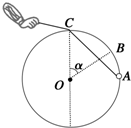
如图所示，固定在竖直平面内的半径为R=0.5m的光滑圆环的最高点C处有一个光滑的小孔，一质量为m=0.1kg的小球套在圆环上，一根细线的一端拴着这个小球，细线的另一端穿过小孔C，手拉细线使小球从A处沿圆环向上移动．在下列两种情况下，当小球通过B处，即∠COB=α=740时，求这两种情况下，细线对小球的拉力F的大小和圆环对小球的弹力FN的大小．（不计空气阻力，g取10m/s2；sin37°=0.6，cos37°=0.8；可能用到