题目内容
4. 一司机驾车在平直公路上以72km/h匀速行驶,当其发现正前方30m处,一人骑自行车以4m/s同向匀速行驶时,决定制动减速,已知该司机的反应时间为0.4s(从作出决定到开始制动的时间),该路段减速过程中汽车位移与速度v的关系曲线如图所示,此过程可视为匀变速直线运动,求:
一司机驾车在平直公路上以72km/h匀速行驶,当其发现正前方30m处,一人骑自行车以4m/s同向匀速行驶时,决定制动减速,已知该司机的反应时间为0.4s(从作出决定到开始制动的时间),该路段减速过程中汽车位移与速度v的关系曲线如图所示,此过程可视为匀变速直线运动,求:(1)该车减速过程的加速度大小;
(2)该车能否避免撞到自行车,计算说明.
分析 (1)根据匀变速直线运动的速度位移公式求出该车减速过程中的加速度大小.
(2)根据速度时间公式求出两车速度相等经历的时间,求出两车速度相等时的位移,从而通过位移关系分析是否能够避免相撞.
解答 解:(1)根据图线知,v=72km/h=20m/s,减速过程的位移x=25m,
根据速度位移公式得,减速过程中的加速度大小a=$\frac{{v}^{2}}{2x}=\frac{400}{2×25}m/{s}^{2}=8m/{s}^{2}$.
(2)当两车速度相等经历的时间$t=\frac{v-v′}{a}=\frac{20-4}{8}s=2s$,
此时汽车的位移${x}_{1}=\frac{{v}^{2}-v{′}^{2}}{2a}=\frac{400-16}{2×8}$m=24m,自行车的位移x2=v′t=4×2m=8m,
因为x1<x2+30m,可知汽车能避免撞到自行车.
答:(1)该车减速过程的加速度大小为8m/s2.
(2)汽车能避免撞到自行车.
点评 本题考查了运动学中的追及问题,关键抓住临界状态,结合速度时的位移关系,运用运动学公式分析判断.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
15.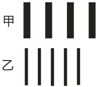 a、b两束单色光分别用同一双缝干涉装置进行实验,在距双缝恒定距离的屏上得到如图所示的干涉图样,图甲是a光照射时形成的干涉图样,图乙是b光照射时形成的干涉图样.下列关于a、b两束单色光的说法正确的是( )
a、b两束单色光分别用同一双缝干涉装置进行实验,在距双缝恒定距离的屏上得到如图所示的干涉图样,图甲是a光照射时形成的干涉图样,图乙是b光照射时形成的干涉图样.下列关于a、b两束单色光的说法正确的是( )
 a、b两束单色光分别用同一双缝干涉装置进行实验,在距双缝恒定距离的屏上得到如图所示的干涉图样,图甲是a光照射时形成的干涉图样,图乙是b光照射时形成的干涉图样.下列关于a、b两束单色光的说法正确的是( )
a、b两束单色光分别用同一双缝干涉装置进行实验,在距双缝恒定距离的屏上得到如图所示的干涉图样,图甲是a光照射时形成的干涉图样,图乙是b光照射时形成的干涉图样.下列关于a、b两束单色光的说法正确的是( )| A. | a光的频率比b光大 | B. | b光比a光易发生衍射现象 | ||
| C. | a光比b光易发生全反射现象 | D. | b光在水中的传播速度较小 |
12.下列表述正确的是( )
| A. | ${\;}_{2}^{4}$H+${\;}_{7}^{14}$N→${\;}_{8}^{17}$O+X中,X表示${\;}_{2}^{3}$He | |
| B. | ${\;}_{1}^{2}$H+${\;}_{1}^{3}$H→${\;}_{2}^{4}$He+${\;}_{0}^{1}$n是重核裂变的核反应方程 | |
| C. | 放射性元素的半衰期与原子所处的化学状态无关 | |
| D. | β衰变中放出的β射线是核外电子挣脱原子核的束缚而形成的 |
19. 如图所示,杂技演员在一根两端周定的水平弹性绳上表演,演员从某一高度下落,落到绳上的A后向下运动,使弹性绳发生形变,B是演员运动到的最低点,不计弹性绳的质量和空气阻力不计,则( )
如图所示,杂技演员在一根两端周定的水平弹性绳上表演,演员从某一高度下落,落到绳上的A后向下运动,使弹性绳发生形变,B是演员运动到的最低点,不计弹性绳的质量和空气阻力不计,则( )
 如图所示,杂技演员在一根两端周定的水平弹性绳上表演,演员从某一高度下落,落到绳上的A后向下运动,使弹性绳发生形变,B是演员运动到的最低点,不计弹性绳的质量和空气阻力不计,则( )
如图所示,杂技演员在一根两端周定的水平弹性绳上表演,演员从某一高度下落,落到绳上的A后向下运动,使弹性绳发生形变,B是演员运动到的最低点,不计弹性绳的质量和空气阻力不计,则( )| A. | 从A到B的运动过程中,演员的机械能保持不变 | |
| B. | 从A到B的运动过程中,演员的动能不断减少 | |
| C. | 从A到B的运动过程中,演员重力做的功等于其重力势能的减小量 | |
| D. | 从A到B的运动过程中,演员重力做的功大于克服绳支持力做的功 |
9.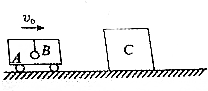 如图所示,小车A内有一用细线悬挂着的小球B,它们相对静止沿光滑水平面向右匀速运动,与原来静止放置在光滑水平面上的物体C发生正碰,碰撞时间极短,碰后A、C粘在一起运动,则( )
如图所示,小车A内有一用细线悬挂着的小球B,它们相对静止沿光滑水平面向右匀速运动,与原来静止放置在光滑水平面上的物体C发生正碰,碰撞时间极短,碰后A、C粘在一起运动,则( )
 如图所示,小车A内有一用细线悬挂着的小球B,它们相对静止沿光滑水平面向右匀速运动,与原来静止放置在光滑水平面上的物体C发生正碰,碰撞时间极短,碰后A、C粘在一起运动,则( )
如图所示,小车A内有一用细线悬挂着的小球B,它们相对静止沿光滑水平面向右匀速运动,与原来静止放置在光滑水平面上的物体C发生正碰,碰撞时间极短,碰后A、C粘在一起运动,则( )| A. | 碰撞瞬间A、C组成的系统机械能守恒 | |
| B. | 碰撞瞬间A、C组成的系统水平方向动量守恒 | |
| C. | 碰撞后的瞬间,细线拉力与小球所受重力大小相等 | |
| D. | 碰撞后的瞬间,细线拉力大于小球所受的重力 |
16.某质点以9.8m/s的初速度做平抛运动,经过一段时间后的末速度为初速度的$\sqrt{3}$,则这段时间是( )(g取9.8m/s2)
| A. | $\sqrt{3}$S | B. | $\sqrt{2}$S | C. | $\frac{\sqrt{3}}{3}$S | D. | $\frac{\sqrt{2}}{2}$S |
14. 如图所示,分界线MN上下两侧有垂直纸面的匀强磁场,磁感应强度分别为B1和B2,一质量为m,电荷为q的带电粒子(不计重力)从O点出发以一定的初速度v0沿纸面垂直MN向上射出,经时间t又回到出发点O,形成了图示心形图案,则( )
如图所示,分界线MN上下两侧有垂直纸面的匀强磁场,磁感应强度分别为B1和B2,一质量为m,电荷为q的带电粒子(不计重力)从O点出发以一定的初速度v0沿纸面垂直MN向上射出,经时间t又回到出发点O,形成了图示心形图案,则( )
 如图所示,分界线MN上下两侧有垂直纸面的匀强磁场,磁感应强度分别为B1和B2,一质量为m,电荷为q的带电粒子(不计重力)从O点出发以一定的初速度v0沿纸面垂直MN向上射出,经时间t又回到出发点O,形成了图示心形图案,则( )
如图所示,分界线MN上下两侧有垂直纸面的匀强磁场,磁感应强度分别为B1和B2,一质量为m,电荷为q的带电粒子(不计重力)从O点出发以一定的初速度v0沿纸面垂直MN向上射出,经时间t又回到出发点O,形成了图示心形图案,则( )| A. | 粒子一定带正电荷 | |
| B. | MN上下两侧的磁场方向相同 | |
| C. | MN上下两侧的磁感应强度的大小B1:B2=1:2 | |
| D. | 时间t=$\frac{2πm}{{qB}_{2}}$ |




