题目内容
17.火星半径约为地球半径的$\frac{1}{2}$,火星质量约为地球质量的$\frac{1}{9}$.地球表面的重力加速度取10m/s2.求:(1)求火星表面的重力加速度.
(2)若弹簧测力计在地球上最多可测出质量是24kg的物体所受的重力,在火星上它最多可测出质量是多大的物体的重力?
分析 (1)由星体表面万有引力等于重力,可得火星与地球表面重力加速度的比值,从而求出火星表面的重力加速度.
(2)根据G=mg求出物体在火星上的重力.
解答 解:(1)由星球表面,由万有引力等于重力得:
mg=G$\frac{Mm}{{R}^{2}}$
则得行星表面的重力加速度为 g=$\frac{GM}{{R}^{2}}$
因此有 $\frac{{g}_{火}}{{g}_{地}}$=$\frac{{M}_{火}}{{M}_{地}}$•$\frac{{R}_{地}^{2}}{{R}_{火}^{2}}$=$\frac{1}{9}$•$\frac{{2}^{2}}{1}$=$\frac{4}{9}$
则火星表面的重力加速度 g火=$\frac{40}{9}$m/s2.
(2)根据弹簧测力计的量程是一定有,则有 m地g地=m火g火,
解得 m火=$\frac{{m}_{地}{g}_{地}}{{g}_{火}}$=$\frac{24×9}{4}$=54kg
答:
(1)火星表面的重力加速度是$\frac{40}{9}$m/s2.
(2)测力计在火星上它最多可测出质量是54kg的物体的重力.
点评 本题的关键明确万有引力与重力的关系,要知道不考虑星球自转时认为万有引力等于重力,由此可研究星球表面重力加速度的关系.

练习册系列答案
相关题目
8. 如图所示,电流表与螺线管组成闭合电路,将条形磁铁分别以速度υ和2υ插入线圈,则电流表指针偏转角度( )
如图所示,电流表与螺线管组成闭合电路,将条形磁铁分别以速度υ和2υ插入线圈,则电流表指针偏转角度( )
 如图所示,电流表与螺线管组成闭合电路,将条形磁铁分别以速度υ和2υ插入线圈,则电流表指针偏转角度( )
如图所示,电流表与螺线管组成闭合电路,将条形磁铁分别以速度υ和2υ插入线圈,则电流表指针偏转角度( )| A. | 第一次大 | B. | 第二次大 | C. | 一样大 | D. | 不能确定 |
12. 如图所示,虚线代表电场中的三个等势面,相邻两个等势面的电势差相等,实线为一带正电的质点仅在电场力作用下通过该区域时的运动轨迹,P、Q为轨迹上的两点,据此可得( )
如图所示,虚线代表电场中的三个等势面,相邻两个等势面的电势差相等,实线为一带正电的质点仅在电场力作用下通过该区域时的运动轨迹,P、Q为轨迹上的两点,据此可得( )
 如图所示,虚线代表电场中的三个等势面,相邻两个等势面的电势差相等,实线为一带正电的质点仅在电场力作用下通过该区域时的运动轨迹,P、Q为轨迹上的两点,据此可得( )
如图所示,虚线代表电场中的三个等势面,相邻两个等势面的电势差相等,实线为一带正电的质点仅在电场力作用下通过该区域时的运动轨迹,P、Q为轨迹上的两点,据此可得( )| A. | 质点从Q到P过程中电场力做正功 | B. | 该质点通过P点时电势能最大 | ||
| C. | 三个等势面中,P点电势最高 | D. | 三个等势面中,Q点电势最高 |
2.关于热力学温标和摄氏温标,下列说法正确的是( )
| A. | 热力学温度与摄氏温度的关系是T=t-273.15K | |
| B. | 热力学温度升高1K大于摄氏温度升高1℃ | |
| C. | 热力学温度升高1K等于摄氏温度升高1℃ | |
| D. | 某物体摄氏温度为10℃,即热力学温度为10K |
9.如图所示为物体分子势能与分子间距离之间的关系,下列判断正确的是( )


| A. | 当r<r0时,r越小,则分子势能Ep越大 | |
| B. | 当r>r0时,r越小,则分子势能Ep越大 | |
| C. | 当r=r0时,分子势能Ep最小 | |
| D. | 当r→∞时,分子势能Ep最小 |
6.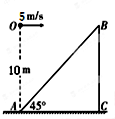 如图所示,斜面与水平面之间的夹角为45°,在斜面底端A点正上方高度为10m处的o点,以5m/s的速度水平抛出一个小球,飞行一段时间后撞在斜面上,这段飞行所用的时间为(g=10m/s2)( )
如图所示,斜面与水平面之间的夹角为45°,在斜面底端A点正上方高度为10m处的o点,以5m/s的速度水平抛出一个小球,飞行一段时间后撞在斜面上,这段飞行所用的时间为(g=10m/s2)( )
 如图所示,斜面与水平面之间的夹角为45°,在斜面底端A点正上方高度为10m处的o点,以5m/s的速度水平抛出一个小球,飞行一段时间后撞在斜面上,这段飞行所用的时间为(g=10m/s2)( )
如图所示,斜面与水平面之间的夹角为45°,在斜面底端A点正上方高度为10m处的o点,以5m/s的速度水平抛出一个小球,飞行一段时间后撞在斜面上,这段飞行所用的时间为(g=10m/s2)( )| A. | 2s | B. | $\sqrt{2}$s | C. | 1s | D. | 0.5s |
7.下列叙述中,正确的是( )
| A. | 汤姆生根据α粒子散射实验,提出了原子的葡萄干布丁模型 | |
| B. | 卢瑟福根据α粒子散射实验,提出了原子的核式结构模型 | |
| C. | 汤姆生最早发现电子 | |
| D. | 卢瑟福最早发现电子 |
 如图所示,带电粒子在“云室”中运动时,可呈现其运动径迹,将“云室”放在匀强电场中,通过观察分析带电粒子的径迹,可以研究原子核发生衰变的规律,现将一静止的放射性原子核放入上述装置中,当它发生衰变时所放射的粒子②与反冲核①经过相等时间所形成的径迹如图所示,已知发生衰变后的瞬间放射出的粒子②和反冲核①的速度方向与电场强度E垂直,图中a、b均表示长度.如果撤掉匀强电场,将“云室”放在匀强磁场中,仍将同种静止的放射性原子核放入上述装置中,若该原子核发生衰变后的瞬间放射出的粒子和反冲核的速度方向也与磁场垂直,求所放射的粒子②与反冲核①的半径之比为多少?
如图所示,带电粒子在“云室”中运动时,可呈现其运动径迹,将“云室”放在匀强电场中,通过观察分析带电粒子的径迹,可以研究原子核发生衰变的规律,现将一静止的放射性原子核放入上述装置中,当它发生衰变时所放射的粒子②与反冲核①经过相等时间所形成的径迹如图所示,已知发生衰变后的瞬间放射出的粒子②和反冲核①的速度方向与电场强度E垂直,图中a、b均表示长度.如果撤掉匀强电场,将“云室”放在匀强磁场中,仍将同种静止的放射性原子核放入上述装置中,若该原子核发生衰变后的瞬间放射出的粒子和反冲核的速度方向也与磁场垂直,求所放射的粒子②与反冲核①的半径之比为多少?