题目内容
13. 如图所示,在xoy平面内,有以O′(R,0)为圆心,R为半径的圆形磁场区域,磁感应强度大小为B,方向垂直xoy平面向外,在y=R上方有范围足够大的匀强电场,方向水平向右,电场强度大小为E.在坐标原点O处有一放射源,可以在xoy平面内向y轴右侧(x>0)发射出速率相同的电子,已知电子在该磁场中的偏转半径也为R,电子量为e,质量为m.不计重力及阻力的作用.
如图所示,在xoy平面内,有以O′(R,0)为圆心,R为半径的圆形磁场区域,磁感应强度大小为B,方向垂直xoy平面向外,在y=R上方有范围足够大的匀强电场,方向水平向右,电场强度大小为E.在坐标原点O处有一放射源,可以在xoy平面内向y轴右侧(x>0)发射出速率相同的电子,已知电子在该磁场中的偏转半径也为R,电子量为e,质量为m.不计重力及阻力的作用.(1)求电子射入磁场时的速度大小;
(2)速度方向沿x轴正方向射入磁场的电子,求它到达y轴所需要的时间
(3)求电子能够射到y轴上的范围.
分析 (1)根据洛伦兹力提供圆周运动的向心力,列式求解速度大小;
(2)电子速度方向沿x轴正方向射入磁场,先做匀速圆周运动,轨迹为$\frac{1}{4}$圆周.射出磁场后,电子做类平抛运动,根据牛顿第二定律和运动学位移公式求解时间.即可求得总时间.
(3)电子在磁场中偏转半径与磁场区域的半径相同,所有电子经过磁场的偏转后都垂直电场射入匀强电场,最远能到达y轴的电子沿着磁场边界运动.由几何关系求解即可.
解答 解:(1)设电子进入磁场的速度为v,由洛伦兹力提供圆周运动的向心力,则有:
evB=$\frac{m{v}^{2}}{R}$
得:v=$\frac{eBR}{m}$
(2)电子速度方向沿x轴正方向射入磁场,先做匀速圆周运动,轨迹为$\frac{1}{4}$圆周,设所用时间为t1.则有:
t1=$\frac{T}{4}$
又 T=$\frac{2πR}{v}$,得:T=$\frac{2πm}{eB}$
解得:t1=$\frac{πm}{2eB}$
射出磁场后,电子做类平抛运动到达y轴,设所用时间为t2.
则有:R=$\frac{1}{2}•\frac{eE}{m}{t}_{2}^{2}$
可得:t2=$\frac{\sqrt{2mR}}{eE}$
所以所求时间为:t=t1+t2=$\frac{πm}{2eB}$+$\frac{\sqrt{2mR}}{eE}$
(3)电子在磁场中偏转的半径同磁场区域的半径,所以所有电子经过磁场的偏转后都能垂直电场射入匀强电场,最远能到达y轴的电子沿着磁场边界运动,最远在y轴上的坐标为:ymax=R+h
又 h=vt,2R=$\frac{eE}{2m}{t}^{2}$
解得:ymax=R+2BR$\sqrt{\frac{eR}{mE}}$
最近的y坐标为:ymin=R
所以能打到的范围是(R,R+2BR$\sqrt{\frac{eR}{mE}}$)
答:(1)电子射入磁场时的速度大小为$\frac{eBR}{m}$;
(2)速度方向沿x轴正方向射入磁场的电子,它到达y轴所需要的时间为$\frac{πm}{2eB}$+$\frac{\sqrt{2mR}}{eE}$.
(3)电子能够射到y轴上的范围是(R,R+2BR$\sqrt{\frac{eR}{mE}}$).
点评 由洛伦兹力提供圆周运动向心力,根据轨迹关系求出电子进入磁场中的速度方向,再根据速度关系求出质子在电场中做何种运动,然后根据运动性质求解.

 如图所示,固定在水平面上的光滑斜面倾角为30°,质量分别为M、m的两个物体通过细绳及轻弹簧连接于光滑轻滑轮两侧,斜面底端有一与斜面垂直的挡板.开始时用手按住物体M,此时M距离挡板的距离为s,滑轮两边的细绳恰好伸直,且弹簧处于原长状态.已知M=2m,空气阻力不计.松开手后,关于二者的运动下列说法中正确的是( )
如图所示,固定在水平面上的光滑斜面倾角为30°,质量分别为M、m的两个物体通过细绳及轻弹簧连接于光滑轻滑轮两侧,斜面底端有一与斜面垂直的挡板.开始时用手按住物体M,此时M距离挡板的距离为s,滑轮两边的细绳恰好伸直,且弹簧处于原长状态.已知M=2m,空气阻力不计.松开手后,关于二者的运动下列说法中正确的是( )| A. | M和m组成的系统机械能守恒 | |
| B. | 当M的速度最大时,m与地面间的作用力为零 | |
| C. | 若M恰好能到达挡板处,则此时m的速度为零 | |
| D. | 若M恰好能到达挡板处,则此过程中重力对M做的功等于弹簧弹性势能的增加量与物体m的机械能增加量之和 |
 如图所示,A、B、C、D是光滑绝缘永平面上一正方形四条边上的四个中点,E、F为CD上的两点,且OE=OF.分别在A、B两点固定等量负电荷,C、D两点固定等量正电荷,一个带正电荷的小球P(设不改变原来电场分布)从E点由静止释放,下列说法中正确的是( )
如图所示,A、B、C、D是光滑绝缘永平面上一正方形四条边上的四个中点,E、F为CD上的两点,且OE=OF.分别在A、B两点固定等量负电荷,C、D两点固定等量正电荷,一个带正电荷的小球P(设不改变原来电场分布)从E点由静止释放,下列说法中正确的是( )| A. | O点的电场强度一定为零 | B. | O点的电势一定为零 | ||
| C. | 小球P从E点移向O点,电势能减小 | D. | 小球P在E、F间做往复运动 |
 如图所示,两块相同的玻璃等腰三棱镜ABC置于空气中,两者的AC面相互平行放置,由红光和蓝光组成的细光束平行于BC面从P点射入,通过两棱镜后,从a、b两点射出.对于从a、b射出的这两束光下列说法正确的是( )
如图所示,两块相同的玻璃等腰三棱镜ABC置于空气中,两者的AC面相互平行放置,由红光和蓝光组成的细光束平行于BC面从P点射入,通过两棱镜后,从a、b两点射出.对于从a、b射出的这两束光下列说法正确的是( )| A. | 从a、b两点射出的两束光不平行 | |
| B. | 从a、b两点射出的两束光仍平行,且平行于BC | |
| C. | 从a点射出的光比从b点射出的光更容易使金属产生光电效应 | |
| D. | 从b点射出的光比从a点射出的光更容易观察到单缝衍射现象 |
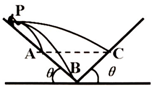 如图所示,在某一峡谷的两侧存在于水平面成相同角度的山坡,某人站在左侧山坡上的P点向对面的山坡上水平抛出三个质量不等的石块,分别落在A,B,C三处,不计空气阻力,A,C两处在同一水平面上,则下列说法正确的是( )
如图所示,在某一峡谷的两侧存在于水平面成相同角度的山坡,某人站在左侧山坡上的P点向对面的山坡上水平抛出三个质量不等的石块,分别落在A,B,C三处,不计空气阻力,A,C两处在同一水平面上,则下列说法正确的是( )| A. | 落到A,B,C三处的石块落地速度方向相同 | |
| B. | 落到A,B两处的石块落地速度方向相同 | |
| C. | 落到B,C两处的石块落地速度大小可能相同 | |
| D. | 落到C处的石块在空中运动的时间最长 |
| A. | ${\;}_{92}^{238}$U→${\;}_{90}^{234}$Th+${\;}_{2}^{4}$He | |
| B. | ${\;}_{1}^{2}$H+${\;}_{1}^{3}$H→${\;}_{2}^{4}$He+${\;}_{0}^{1}$n | |
| C. | ${\;}_{4}^{9}$Be+${\;}_{2}^{4}$He→${\;}_{6}^{12}$C+${\;}_{0}^{1}$n | |
| D. | ${\;}_{92}^{235}$U+${\;}_{0}^{1}$n→${\;}_{56}^{141}$Ba+${\;}_{36}^{92}$Kr+3${\;}_{0}^{1}$n |
| A. | 物理学家奥斯特发现了由磁场产生电流的条件和规律 | |
| B. | 物理学家亨利发现自感现象,日光灯的工作原理中应用了自感现象 | |
| C. | 物理学家麦克斯韦用实验证实了电磁波的存在,指出光是一种电磁波 | |
| D. | 物理学家安培发现两根通有同向电流的平行导线相斥,反向电流的平行导线则相吸 |
 如图甲所示,竖直平行放置的金属板A、B的电压为U0,中心各有一个小孔P、Q.水平平行放置的金属板C、D间电压的变化规律如图乙所示,板长和板间距均为L,粒子的接收屏M与D板间夹角为127°,现从P点处连续不断的有质量为m,带电量为+q的粒子放出(粒子的初速度可忽略不计),经加速电场AB加速后从Q点水平射出,紧贴着C板的下侧并平行C板射入C、D板间的匀强电场(边缘外没有电场),经过一个周期后,粒子恰好通过C、D间的电场,不计粒子间的相互作用力,重力不计,sin37°=0.6,cos37°=0.8.求:
如图甲所示,竖直平行放置的金属板A、B的电压为U0,中心各有一个小孔P、Q.水平平行放置的金属板C、D间电压的变化规律如图乙所示,板长和板间距均为L,粒子的接收屏M与D板间夹角为127°,现从P点处连续不断的有质量为m,带电量为+q的粒子放出(粒子的初速度可忽略不计),经加速电场AB加速后从Q点水平射出,紧贴着C板的下侧并平行C板射入C、D板间的匀强电场(边缘外没有电场),经过一个周期后,粒子恰好通过C、D间的电场,不计粒子间的相互作用力,重力不计,sin37°=0.6,cos37°=0.8.求: 如图所示的电路中,L是自感系数足够大的线圈,它的电阻可忽略不计,L1和L2是两个完全不同的小灯泡.问:
如图所示的电路中,L是自感系数足够大的线圈,它的电阻可忽略不计,L1和L2是两个完全不同的小灯泡.问: