题目内容
5. 两个质量相同的小球用不可伸长的长为L的绝缘细线连结,置于场强为E的匀强电场中,小球1和小球2均带负电,电量分别为q1和q2(q1>q2),将细线拉直并使之与电场方向平行,如图所示,若将两球同时从静止状态释放,则释放后细线中的张力T为( )(不计重力,线长L远大于小球的线度)
两个质量相同的小球用不可伸长的长为L的绝缘细线连结,置于场强为E的匀强电场中,小球1和小球2均带负电,电量分别为q1和q2(q1>q2),将细线拉直并使之与电场方向平行,如图所示,若将两球同时从静止状态释放,则释放后细线中的张力T为( )(不计重力,线长L远大于小球的线度)| A. | T=(q2-q1)E+$\frac{k{q}_{1}{q}_{2}}{{L}^{2}}$ | B. | T=$\frac{1}{2}$(q2-q1)E+$\frac{k{q}_{1}{q}_{2}}{{L}^{2}}$ | ||
| C. | T=$\frac{1}{2}$(q2-q1)E-$\frac{k{q}_{1}{q}_{2}}{{L}^{2}}$ | D. | T=(q2+q1)E+$\frac{k{q}_{1}{q}_{2}}{{L}^{2}}$ |
分析 对球1、2整体受力分析,根据牛顿第二定律求出整体的加速度.
对球2受力分析,由牛顿第二定律求出细线中的张力T.
解答 解:对球1、2整体受力分析,根据牛顿第二定律得:
Eq1+Eq2=2ma,
对球2受力分析,由牛顿第二定律与库仑定律,可得:
T-$\frac{k{q}_{1}{q}_{2}}{{L}^{2}}$+Eq1=ma,
两式联立得T=$\frac{1}{2}$(q2-q1)E+$\frac{k{q}_{1}{q}_{2}}{{L}^{2}}$,故B正确,ACD错误;
故选:B.
点评 解决本题关键在于把牛顿第二定律和电场力知识结合起来,在研究对象上能学会整体法和隔离法的应用.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
5.关于曲线运动,下列说法正确的是( )
| A. | 曲线运动一定是变速运动,但速度的大小可以不变 | |
| B. | 曲线运动的加速度可以是不变的 | |
| C. | 曲线运动的速度的大小及方向一定在变化 | |
| D. | 曲线运动的速度的方向一定在变化,在某一点瞬时速度的方向与质点运动方向成一定角度 |
16. 氢原子能级示意图如图所示,不同色光的光子能量如表所示.
氢原子能级示意图如图所示,不同色光的光子能量如表所示.
则 ( )
 氢原子能级示意图如图所示,不同色光的光子能量如表所示.
氢原子能级示意图如图所示,不同色光的光子能量如表所示.| 色光 | 红 | 橙 | 黄 | 绿 | 蓝-靛 | 紫 |
| 光子能量范围(eV) | 1.61-2.00 | 2.00-2.07 | 2.07-2.14 | 2.14-2.53 | 2.53-2.76 | 2.76-3.10 |
| A. | 氢原子从n=3能级向n=2能级跃迁时产生的光是红色 | |
| B. | 氢原子从n=4能级向n=3能级跃迁时产生的光是红色 | |
| C. | 氢原子从n=4能级向n=2能级跃迁时产生的光是蓝一靛 | |
| D. | 用绿光照射逸出功为2.25eV的钾表面,可能产生光电效应 | |
| E. | 用紫光照射逸出功为2.25eV的钾表面,不能产生光电效应 |
20.如图甲所示,有一绝缘的竖直圆环,圆环上均匀分布着正电荷.一光滑细杆沿垂直圆环平面的轴线穿过圆环,细杆上套有一个质量为m=10g的带正电的小球,小球所带电荷量q=5.0×10-4C,让小球从C点由静止释放,其沿细杆由C经B向A运动的v-t图象如图乙所示.且已知小球运动到B点时,速度图象的切线斜率最大(图中标出了该切线).下列说法正确的是( )
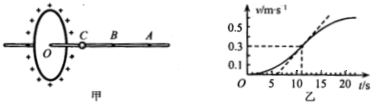

| A. | 在O点右侧杆上,B点场强最大,场强大小为E=1.2V/m | |
| B. | 由C到A的过程中,小球的电势能先减小后变大 | |
| C. | 沿着C到A的方向,电势先降低后升高 | |
| D. | C、B两点间的电势差UCB=0.9V |
17.火星探测项目是我国继神舟载人航天工程嫦娥探月工程之后又一个重大太空探索项目,已知地球的质量约为火星质量的10倍,地球的半径约为火星半径的2倍,则下列判断正确的是( )
| A. | 同一探测器在火星表面的重力比在地球表面的重力要小 | |
| B. | 火星的第一宇宙速度一定大于地球的第一宇宙速度 | |
| C. | 若探测器绕火星和绕地球做匀速圆周运动的半径相同,则其线速度相同 | |
| D. | 若探测器绕火星和绕地球做匀速圆周运动的半径相同,则其周期相同 |
14. 足球比赛中踢点球时,足球距球门10.97m,球正对球门踢出后恰好沿水平方向从横梁的下沿擦进球门,已知足球质量为400g,不计空气阻力,则该球员在此次踢球过程中对足球做的功约为( )
足球比赛中踢点球时,足球距球门10.97m,球正对球门踢出后恰好沿水平方向从横梁的下沿擦进球门,已知足球质量为400g,不计空气阻力,则该球员在此次踢球过程中对足球做的功约为( )
 足球比赛中踢点球时,足球距球门10.97m,球正对球门踢出后恰好沿水平方向从横梁的下沿擦进球门,已知足球质量为400g,不计空气阻力,则该球员在此次踢球过程中对足球做的功约为( )
足球比赛中踢点球时,足球距球门10.97m,球正对球门踢出后恰好沿水平方向从横梁的下沿擦进球门,已知足球质量为400g,不计空气阻力,则该球员在此次踢球过程中对足球做的功约为( )| A. | 30J | B. | 60J | C. | 90J | D. | 120J |
15. 假设在宇宙中存在这样的三个天体a、b、c,如图所示,天体a和b以相同角速度绕天体c做匀速圆周运动.以下说法正确的是( )
假设在宇宙中存在这样的三个天体a、b、c,如图所示,天体a和b以相同角速度绕天体c做匀速圆周运动.以下说法正确的是( )
 假设在宇宙中存在这样的三个天体a、b、c,如图所示,天体a和b以相同角速度绕天体c做匀速圆周运动.以下说法正确的是( )
假设在宇宙中存在这样的三个天体a、b、c,如图所示,天体a和b以相同角速度绕天体c做匀速圆周运动.以下说法正确的是( )| A. | 天体a做圆周运动的加速度大于天体b做圆周运动的加速度 | |
| B. | 天体a做圆周运动的速度小于天体b做圆周运动的速度 | |
| C. | 天体b做圆周运动的向心力大于天体c对它的万有引力 | |
| D. | 天体b做圆周运动的向心力由天体a和天体c对它的万有引力共同提供 |
 如图,足够长的光滑平行金属导轨电阻不计,间距L=1m,与水平成成θ=37°角倾斜放置,导轨上端连有阻值R=2Ω的电阻,磁感应强度B=1T的匀强磁场垂直于导轨平面.现有质量m=1kg、电阻r=3Ω的金属棒,从导轨上x=0处以初速度v0=10m/s沿导轨向上运动,对金属棒施加一个平行于导轨平面向上做匀减速运动的过程中,每1s内在电阻R上的电压变化总是2V,已知g=10m/s2,sin37°=0.6.求
如图,足够长的光滑平行金属导轨电阻不计,间距L=1m,与水平成成θ=37°角倾斜放置,导轨上端连有阻值R=2Ω的电阻,磁感应强度B=1T的匀强磁场垂直于导轨平面.现有质量m=1kg、电阻r=3Ω的金属棒,从导轨上x=0处以初速度v0=10m/s沿导轨向上运动,对金属棒施加一个平行于导轨平面向上做匀减速运动的过程中,每1s内在电阻R上的电压变化总是2V,已知g=10m/s2,sin37°=0.6.求


