题目内容
20. 如图所示,“T”形活塞将绝热气缸内的气体分隔成A、B两部分,活塞左右两侧截面积分别为S1、S2,活塞至气缸两端底部的距离均为L,活塞与缸壁间无摩擦.气缸上a、b两个小孔用细管(容积不计)连通.初始时缸内气体的压强等于外界大气压强P0,温度为T0.现对缸内气体缓慢加热,发现活塞向右移动了△L的距离(活塞移动过程中不会经过小孔),求缸内气体的温度.
如图所示,“T”形活塞将绝热气缸内的气体分隔成A、B两部分,活塞左右两侧截面积分别为S1、S2,活塞至气缸两端底部的距离均为L,活塞与缸壁间无摩擦.气缸上a、b两个小孔用细管(容积不计)连通.初始时缸内气体的压强等于外界大气压强P0,温度为T0.现对缸内气体缓慢加热,发现活塞向右移动了△L的距离(活塞移动过程中不会经过小孔),求缸内气体的温度.
分析 对活塞,受两侧气体的压力和外界大气压力,根据平衡条件列式判断出气压情况,然后根据盖•吕萨克定律列式求解即可.
解答 解:设末态时缸内气体的压强为P,体积为V,温度为T,以活塞为研究对象:
P(S1-S2)=P0(S1-S2)
即:P=P0
由盖•吕萨克定律:$\frac{{V}_{0}}{{T}_{0}}=\frac{V}{T}$
式中:V0=(S1+S2)L
V=(S1+S2)L+(S1-S2)•△L
联立解得:
T=[1+$\frac{({S}_{1}-{S}_{2})•△L}{({S}_{1}+{S}_{2})L}$]T0
答:缸内气体的温度为[1+$\frac{({S}_{1}-{S}_{2})•△L}{({S}_{1}+{S}_{2})L}$]T0.
点评 本题关键是对活塞受力分析后求解出内部气压,然后根据盖•吕萨克定律列式求解,基础题目.

练习册系列答案
相关题目
5.下列说法正确的是( )
| A. | 重核裂变和轻核的聚变过程都有质量亏损,都向外界放出核能 | |
| B. | 氢原子从n=3的能级向低能级跃迁时只会辐射出两种不同频率的光 | |
| C. | 比结合能大的原子核分解成比结合能小的原子核时要吸收能量 | |
| D. | β衰变中产生的β射线实际上是原子的核外电子挣脱原子核的束缚而形成的 |
15. 如图所示,一固定的细直杆与水平面的夹角为α=15°,一个质量忽略不计的小轻环C套在直杆上,一根轻质细线的两端分别固定于直杆上的A、B两点,细线依次穿过小环甲、小轻环C和小环乙,且小环甲和小环乙分居在小轻环C的两侧.调节A、B间细线的长度,当系统处于静止状态时β=45°.不计一切摩擦.设小环甲的质量为m1,小环乙的质量为m2,则m1:m2等于( )
如图所示,一固定的细直杆与水平面的夹角为α=15°,一个质量忽略不计的小轻环C套在直杆上,一根轻质细线的两端分别固定于直杆上的A、B两点,细线依次穿过小环甲、小轻环C和小环乙,且小环甲和小环乙分居在小轻环C的两侧.调节A、B间细线的长度,当系统处于静止状态时β=45°.不计一切摩擦.设小环甲的质量为m1,小环乙的质量为m2,则m1:m2等于( )
 如图所示,一固定的细直杆与水平面的夹角为α=15°,一个质量忽略不计的小轻环C套在直杆上,一根轻质细线的两端分别固定于直杆上的A、B两点,细线依次穿过小环甲、小轻环C和小环乙,且小环甲和小环乙分居在小轻环C的两侧.调节A、B间细线的长度,当系统处于静止状态时β=45°.不计一切摩擦.设小环甲的质量为m1,小环乙的质量为m2,则m1:m2等于( )
如图所示,一固定的细直杆与水平面的夹角为α=15°,一个质量忽略不计的小轻环C套在直杆上,一根轻质细线的两端分别固定于直杆上的A、B两点,细线依次穿过小环甲、小轻环C和小环乙,且小环甲和小环乙分居在小轻环C的两侧.调节A、B间细线的长度,当系统处于静止状态时β=45°.不计一切摩擦.设小环甲的质量为m1,小环乙的质量为m2,则m1:m2等于( )| A. | tan15° | B. | tan30° | C. | tan60° | D. | tan75° |
5.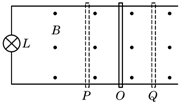 如图所示,接有灯泡L(阻值为R)的平行金属导轨(间距为l,电阻忽略不计)水平放置在磁感应强度为B的匀强磁场中.在外力F的作用下,一电阻可忽略的导体杆与两导轨良好接触并在P、Q两位置间做往复运动.从杆通过O位置,并沿OP方向运动时开始计时,其运动的速度-时间关系为v=v0cosωt,则下列说法中正确的是( )
如图所示,接有灯泡L(阻值为R)的平行金属导轨(间距为l,电阻忽略不计)水平放置在磁感应强度为B的匀强磁场中.在外力F的作用下,一电阻可忽略的导体杆与两导轨良好接触并在P、Q两位置间做往复运动.从杆通过O位置,并沿OP方向运动时开始计时,其运动的速度-时间关系为v=v0cosωt,则下列说法中正确的是( )
 如图所示,接有灯泡L(阻值为R)的平行金属导轨(间距为l,电阻忽略不计)水平放置在磁感应强度为B的匀强磁场中.在外力F的作用下,一电阻可忽略的导体杆与两导轨良好接触并在P、Q两位置间做往复运动.从杆通过O位置,并沿OP方向运动时开始计时,其运动的速度-时间关系为v=v0cosωt,则下列说法中正确的是( )
如图所示,接有灯泡L(阻值为R)的平行金属导轨(间距为l,电阻忽略不计)水平放置在磁感应强度为B的匀强磁场中.在外力F的作用下,一电阻可忽略的导体杆与两导轨良好接触并在P、Q两位置间做往复运动.从杆通过O位置,并沿OP方向运动时开始计时,其运动的速度-时间关系为v=v0cosωt,则下列说法中正确的是( )| A. | 杆中电流与时间的关系为i=$\frac{Bl{v}_{0}cosωt}{R}$ | |
| B. | 杆所受安培力与时间的关系为FA=$\frac{{B}^{2}{l}^{2}{v}_{0}sinωt}{R}$ | |
| C. | 杆克服安培力做功的功率与时间的关系为p=$\frac{(Bl{v}_{0}cosωt)^{2}}{R}$ | |
| D. | 杆运动一个周期,回路中产生的焦耳热为Q=$\frac{{B}^{2}{l}^{2}{{v}_{0}}^{2}π}{Rω}$ |
9.如图所示,AB间的电压为30V,移动滑动变阻器触头P,可以改变CD间的电压,UCD的变化范围是( )


| A. | 0~10V | B. | 0~20V | C. | 10~20V | D. | 20V~30V |
10.下列关于近代物理知识的描述中,正确的是( )
| A. | 处于n=3能级状态的大量氢原子自发跃迁时,能发出3种频率的光子 | |
| B. | β射线实际上是原子的核外电子挣脱原子核的束缚而形成的 | |
| C. | 在${\;}_{7}^{14}$N+${\;}_{2}^{4}$He→${\;}_{0}^{17}$O+X核反应中,X是质子,这个反应过程叫α衰变 | |
| D. | 原子核所含核子单独存在时的总质量大于该原子核的质量 |
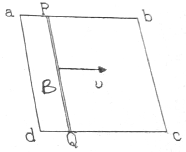 如图所示的正方形线框abcd边长为l,线圈水平放置,固定在磁感应强度为B,方向垂直的匀强磁场,其中ab边是电阻为R的匀强电阻丝,其余三边电阻不计,现有一段长度、粗细、材料均匀与ab边相同的电阻丝PQ架在线框上,并受到与ab平行的恒定水平力F作用从ad边由静止开始滑向bc边,PQ在滑动中与线框接触良好,摩擦阻力忽略不计,PQ电阻丝的质量为m,当PQ滑过$\frac{L}{3}$的距离时,它加速运动的加速度为a.
如图所示的正方形线框abcd边长为l,线圈水平放置,固定在磁感应强度为B,方向垂直的匀强磁场,其中ab边是电阻为R的匀强电阻丝,其余三边电阻不计,现有一段长度、粗细、材料均匀与ab边相同的电阻丝PQ架在线框上,并受到与ab平行的恒定水平力F作用从ad边由静止开始滑向bc边,PQ在滑动中与线框接触良好,摩擦阻力忽略不计,PQ电阻丝的质量为m,当PQ滑过$\frac{L}{3}$的距离时,它加速运动的加速度为a.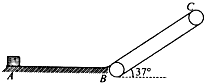 如图所示为仓库中常用的皮带传输装置示意图.传送带BC与水平平台AB的夹角θ=37°,其交接处由很小的圆弧平滑连接,平台左端A处一质量为m=30kg的货物,在F=350N水平推力的作用下由静止开始向传送带运动,经时间t1=1.5s到达平台AB的中点,此时撤去外力F,货物继续向前运动,不计货物经过B处的机械能损失.已知货物与平台和传送带间的动摩擦因数均为0.5,B、C两端相距4.45m,g=10m/s2,cos37°=0.8,sin37°=0.6.求:
如图所示为仓库中常用的皮带传输装置示意图.传送带BC与水平平台AB的夹角θ=37°,其交接处由很小的圆弧平滑连接,平台左端A处一质量为m=30kg的货物,在F=350N水平推力的作用下由静止开始向传送带运动,经时间t1=1.5s到达平台AB的中点,此时撤去外力F,货物继续向前运动,不计货物经过B处的机械能损失.已知货物与平台和传送带间的动摩擦因数均为0.5,B、C两端相距4.45m,g=10m/s2,cos37°=0.8,sin37°=0.6.求: 如图,半径R=1m的$\frac{3}{4}$圆形光滑管道ABC竖直放在水平地面上,C为最高点,B为最低点,管道内放一可在管道内自由移动的小球,现对管道施加一水平向右的恒力F,小球恰好可以在P点相对管道静止,此时过P点的半径OP与竖直方向的夹角为θ=30°,现再用这一装置将小球锁定在B点,管道仍在恒力F作用下从静止开始沿水平地面向右做匀加速运动,经过一段时间后管道遇一障碍突然停止运动,同时解除锁定,小球能通过管道的A点,重力加速度为g=10m/s2,小球及管道大小不计.求:
如图,半径R=1m的$\frac{3}{4}$圆形光滑管道ABC竖直放在水平地面上,C为最高点,B为最低点,管道内放一可在管道内自由移动的小球,现对管道施加一水平向右的恒力F,小球恰好可以在P点相对管道静止,此时过P点的半径OP与竖直方向的夹角为θ=30°,现再用这一装置将小球锁定在B点,管道仍在恒力F作用下从静止开始沿水平地面向右做匀加速运动,经过一段时间后管道遇一障碍突然停止运动,同时解除锁定,小球能通过管道的A点,重力加速度为g=10m/s2,小球及管道大小不计.求: