题目内容
17.图1是验证机械能守恒定律的实验.小圆柱由一根不可伸长的细线拴住,细线另一端固定在O点,在最低点附近放置一组光电门.将细线拉至水平后由静止释放,用光电门测出小圆柱运动到最低点的挡光时间△t,再用10分度游标卡尺测出小圆柱的直径d,如图2所示,重力加速度为g.则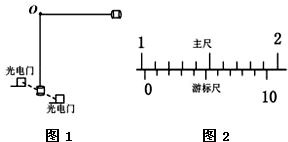
(1)小圆柱的直径d=1.02cm;
(2)测出悬点到圆柱重心的距离l,若等式gl=$\frac{{d}^{2}}{{2(△t)}^{2}}$成立,说明小圆柱下摆过程机械能守恒;
(3)若在悬点O安装一个拉力传感器,测出绳子上的拉力F,则验证小圆柱作圆周运动在最低点向心力的公式还需要测量的物理量是小圆柱的质量m(用文字和字母表示),若等式F=mg+m$\frac{{md}^{2}}{{l(△t)}^{2}}$成立,则可验证小圆柱作圆周运动在最低点向心力的公式.
分析 (1)题读数时注意分度,读数时要用“mm”为单位.
(2)的关键是根据机械能守恒定律列出表达式即可.
(3)题的关键是根据牛顿第二定律列出表达式,然后求出拉力表达式即可.
解答 解:(1)游标卡尺读数为:d=10mm+2×0.1mm=10.2mm=1.02cm
(2)根据机械能守恒定律应有:mgl=$\frac{1}{2}$mv2,
其中:v=$\frac{d}{△t}$,解得:gl=$\frac{1}{2}$${(\frac{d}{△t})}^{2}$=$\frac{{d}^{2}}{{2(△t)}^{2}}$
(3)根据牛顿第二定律有:F-mg=m$\frac{{v}^{2}}{l}$,
解得:F=mg+$\frac{{md}^{2}}{{l(△t)}^{2}}$,可见还需要测量小圆柱的质量m,才能求出绳子的拉力.
故答案为:(1)1.02;(2)$\frac{{d}^{2}}{{2(△t)}^{2}}$;(3)小圆柱的质量m,mg+$\frac{{md}^{2}}{{l(△t)}^{2}}$
点评 遇到实验问题,关键是明确实验原理,根据物理规律列出相应方程,然后求解讨论即可.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
7. 质量为m的小球由轻绳a和b系于一轻质木架上的A点和C点,且La<Lb,如图所示.当轻杆绕轴BC以角速度ω匀速转动时,小球在水平面内作匀速圆周运动,绳a在竖直方向、绳b在水平方向.当小球运动在图示位置时,绳b被烧断的同时杆也停止转动,则( )
质量为m的小球由轻绳a和b系于一轻质木架上的A点和C点,且La<Lb,如图所示.当轻杆绕轴BC以角速度ω匀速转动时,小球在水平面内作匀速圆周运动,绳a在竖直方向、绳b在水平方向.当小球运动在图示位置时,绳b被烧断的同时杆也停止转动,则( )
 质量为m的小球由轻绳a和b系于一轻质木架上的A点和C点,且La<Lb,如图所示.当轻杆绕轴BC以角速度ω匀速转动时,小球在水平面内作匀速圆周运动,绳a在竖直方向、绳b在水平方向.当小球运动在图示位置时,绳b被烧断的同时杆也停止转动,则( )
质量为m的小球由轻绳a和b系于一轻质木架上的A点和C点,且La<Lb,如图所示.当轻杆绕轴BC以角速度ω匀速转动时,小球在水平面内作匀速圆周运动,绳a在竖直方向、绳b在水平方向.当小球运动在图示位置时,绳b被烧断的同时杆也停止转动,则( )| A. | 小球仍在水平面内作匀速圆周运动 | |
| B. | 在绳被烧断瞬间,a绳中张力不变 | |
| C. | 在绳被烧断瞬间,小球所受的合外力突然变小 | |
| D. | 若角速度ω较大,小球可以在竖直平面内作圆周运动 |
2.CTMD(中国战区导弹防御体系)是一种战术型导弹防御系统,可以拦截各类型的短程及中程超音速导弹.在某次演习中,检测系统测得关闭发动机的导弹在距地面高为H处,其速度为v且恰好水平,反应灵敏的地面拦截系统同时以初速度v0竖直向上发射一颗炮弹成功拦截.已知发射时炮弹与导弹的水平距离为s,不计空气阻力,则( )
| A. | v0=$\frac{H}{s}$v | B. | v0=$\sqrt{\frac{H}{s}}$v | C. | v0=$\frac{s}{H}$v | D. | v0=v |
9. 如图所示的电路中,定值电阻的阻值为10Ω,电动机M的线圈电阻值为2Ω,a、b两端加有44V的恒定电压,理想电压表的示数为24伏,由此可知( )
如图所示的电路中,定值电阻的阻值为10Ω,电动机M的线圈电阻值为2Ω,a、b两端加有44V的恒定电压,理想电压表的示数为24伏,由此可知( )
 如图所示的电路中,定值电阻的阻值为10Ω,电动机M的线圈电阻值为2Ω,a、b两端加有44V的恒定电压,理想电压表的示数为24伏,由此可知( )
如图所示的电路中,定值电阻的阻值为10Ω,电动机M的线圈电阻值为2Ω,a、b两端加有44V的恒定电压,理想电压表的示数为24伏,由此可知( )| A. | 通过电动机的电流为12A | |
| B. | 电动机消耗的功率为288W | |
| C. | 电动机的线圈在1min内产生的热量为480J | |
| D. | 电动机的输出功率为8W |
6.霍尔元件可作为传感器使用,霍尔元件能转换哪两个量( )
| A. | 把磁感应强度这个磁学量转换为电压这个电学量 | |
| B. | 把温度这个热学量转换为电阻这个电学量 | |
| C. | 把力转换为电压这个电学量 | |
| D. | 把光照强弱这个光学量转换为电阻这个电学量 |
7. 如图所示,墙壁与斜面体的接触面处处相同,用垂直于斜面的力推着斜面体沿着竖直固定墙壁匀速下滑,下列说法正确的是( )
如图所示,墙壁与斜面体的接触面处处相同,用垂直于斜面的力推着斜面体沿着竖直固定墙壁匀速下滑,下列说法正确的是( )
 如图所示,墙壁与斜面体的接触面处处相同,用垂直于斜面的力推着斜面体沿着竖直固定墙壁匀速下滑,下列说法正确的是( )
如图所示,墙壁与斜面体的接触面处处相同,用垂直于斜面的力推着斜面体沿着竖直固定墙壁匀速下滑,下列说法正确的是( )| A. | 如果减小推力,斜面体一定减速下滑 | |
| B. | 如果减小推力,斜面体仍然匀速下滑 | |
| C. | 如果増大推力,斜面体一定加速下滑 | |
| D. | 如果增大推力,斜面体一定减速下滑 |