题目内容
质量为0.5kg的小球，以v=20m?s-1的初速度竖直向上从地面射出，它只上升了高度h=18m，如果小球在运动中所受到的空气阻力大小不变，并取g=10m/s2，那么小球在什么位置时重力势能和动能相等？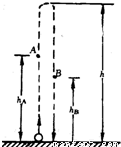
【答案】分析：根据动能定理来确定空气受到的阻力，再由动能与势能相等，结合动能定理，即可求出重力势能和动能相等的位置．
解答：解：因为阻力存在，小球在运动过程中机械能不断减少，如图，如果在上升阶段中位于A处时球的动能和势能相等，那么到下落阶段球运动到A处，其动能就一定会小于势能，因此，与无阻力的竖直上抛运动不同，这里球在上升中的动能和势能相等的点A与球在下降中的动能和势能相等的点B并不在同一点．
设小球在运动中受到空气阻力的大小为f，则对于球的上升过程，由动能定理有
-（mg+f）h=0-
mv2
∴f=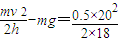
N-0.5×10N=
N
设上升过程中球在A点处动能与势能相等，以hA表增A点的高度，VA表示球在A点时的速度，则有
mghA=
mv2
而由动能定理又有
-（mg+f）hA=
mv2-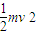
由上两式可解得
hA=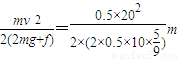
=9.47m
又设下落过程中球在B点处动能与势能相等，以hB表示B点的高度，vB表示球在B点时的速度，
则有 mghB=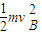
对于球自最高点下落至B点的过程，由动能定理有
mg（h-hB）-f（h-hB）=
mv2
由上两式可解得
hB=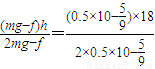
m=8.47m
答：小球在8.47m处的位置时重力势能和动能相等．
点评：考查动能定理的应用，掌握重力势能的参考平面的选择．同时注意做功的正负值．
解答：解：因为阻力存在，小球在运动过程中机械能不断减少，如图，如果在上升阶段中位于A处时球的动能和势能相等，那么到下落阶段球运动到A处，其动能就一定会小于势能，因此，与无阻力的竖直上抛运动不同，这里球在上升中的动能和势能相等的点A与球在下降中的动能和势能相等的点B并不在同一点．
设小球在运动中受到空气阻力的大小为f，则对于球的上升过程，由动能定理有
-（mg+f）h=0-
mv2∴f=
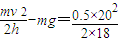N-0.5×10N=N 设上升过程中球在A点处动能与势能相等，以hA表增A点的高度，VA表示球在A点时的速度，则有
mghA=
mv2而由动能定理又有
-（mg+f）hA=
mv2-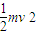由上两式可解得
hA=
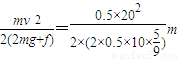=9.47m 又设下落过程中球在B点处动能与势能相等，以hB表示B点的高度，vB表示球在B点时的速度，
则有 mghB=
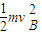
对于球自最高点下落至B点的过程，由动能定理有
mg（h-hB）-f（h-hB）=
mv2由上两式可解得
hB=
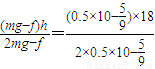m=8.47m 答：小球在8.47m处的位置时重力势能和动能相等．
点评：考查动能定理的应用，掌握重力势能的参考平面的选择．同时注意做功的正负值．
练习册系列答案
名校课堂系列答案
相关题目
（2008?卢湾区模拟）如图所示，一块质量为0.6kg均匀平板AB长0.8m，其左端搁在水平地面上，板与地面的夹角为370，板中心C垂直固定在轻支架上，支架长OC为0.3m，支架下端与水平固定转轴O连接．在平板A点处有一质量为0.5kg的小物体m以初速v0沿板向上运动，物体与平板间的动摩擦因数为0.2，g取10m/s2．试求：
如图，有一半径为R=0.3m的光滑半圆形细管AB，将其固定在竖直墙面并使B端切线水平．一个可视为质点的质量为0.5Kg的小物体m由细管上端沿A点切线方向进入细管，从B点以速度VB=4.0m/s飞出后，恰好能从一倾角为θ=37°的倾斜传送带顶端C无碰撞的滑上传送带．已知传送带长度为L=2.75m（图中只画出了传送带的部分示意图），物体与传送带之间的动摩擦因数为u=0.50，（取sin37°=0.60，cos37°=0.80，g=10m/s2，不计空气阻力，不考虑半圆形管AB的内径）．
如图所示，传送带保持1m/s的速率运动，现将一质量为0.5kg的小物体放在传送带A端，物体初速度为零，设物体与传送带间的动摩擦因素为0.1，传送带AB两端的距离为2.5m，AB距离水平地面的高度为H=0.45m．求：
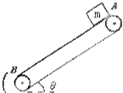如图所示，传送带与地面倾角θ=37°，从A到B长度为16m，传送带以10m/s的恒定速率针转动，在传送带上端A处无初速度放一个质量为0.5kg的小物体，它与传送带的摩擦系数为0.5，其它摩擦不计，已知sin37°=0.6，cos37°=0.8，g取10m/s2．求：（1）若传送带顺时针转动，物体由A滑到B的时间？