题目内容
4. 长为L的轻绳一端固定于O点,另一端系质量为m的小球,把小球拉离水平方向上方至绳与水平方向成α=30°时静止释放,当小球自由下落并摆至最低点时绳的张力F为(已知重力加速度为g)( )
长为L的轻绳一端固定于O点,另一端系质量为m的小球,把小球拉离水平方向上方至绳与水平方向成α=30°时静止释放,当小球自由下落并摆至最低点时绳的张力F为(已知重力加速度为g)( )| A. | 4mg | B. | 3.5mg | C. | 3mg | D. | 2.5mg |
分析 小球从开始下落到细线绷紧前做自由落体运动,遵守机械能守恒,根据机械能守恒定律可求解细线刚拉紧时的速度大小;细线绷紧瞬间沿细线方向的速度突然减至零,只有垂直于细线的分速度,将速度分解得到圆周运动的初速度,再由机械能守恒求得小球运动到最低点时的速度,由牛顿第二定律求解张力.
解答 解:小球先做自由落体运动,设细线刚拉紧时的速度大小为v1.根据机械能守恒定律得:
mgL=$\frac{1}{2}$m${v}_{1}^{2}$,解得 v1=$\sqrt{2gL}$
拉紧细线后瞬间,小球的速度设为v2,根据运动的分解得:
v2=v1cos30°=$\sqrt{\frac{3}{2}gL}$
设小球运动到最低点A时的速度为v3.根据机械能守恒定律得:
$\frac{1}{2}m{v}_{3}^{2}$=mgL(1-sin30°)+$\frac{1}{2}m{v}_{2}^{2}$
解得 v3=$\sqrt{\frac{5}{2}gL}$
在最低点,由牛顿第二定律得:
T-mg=m$\frac{{v}_{3}^{2}}{L}$,解得 T=3.5mg
故选:B.
点评 解决本题的关键要把握住细线绷紧前后速度的变化,要注意中学阶段的细线是刚性的,不可伸长,细线绷紧瞬间沿细线方向的速度突然减至零.

练习册系列答案
相关题目
9. 如图所示,现有四条完全相同的垂直于纸面放置的长直导线,横截面分别位于一正方形abcd的四个顶点上,直导线分别通有方向垂直纸面向里、大小分别为Ia=1A,Ib=2A,Ic=3A和Id=4A的恒定电流,已知离通电长导线相同距离的点,磁感应强度的大小与电流大小成正比,忽略电流间的相互作用,若电流Ia在正方形的几何中心O点处产生的磁感应强度大小为1T,则O点处实际的磁感应强度的大小及方向分别为( )
如图所示,现有四条完全相同的垂直于纸面放置的长直导线,横截面分别位于一正方形abcd的四个顶点上,直导线分别通有方向垂直纸面向里、大小分别为Ia=1A,Ib=2A,Ic=3A和Id=4A的恒定电流,已知离通电长导线相同距离的点,磁感应强度的大小与电流大小成正比,忽略电流间的相互作用,若电流Ia在正方形的几何中心O点处产生的磁感应强度大小为1T,则O点处实际的磁感应强度的大小及方向分别为( )
 如图所示,现有四条完全相同的垂直于纸面放置的长直导线,横截面分别位于一正方形abcd的四个顶点上,直导线分别通有方向垂直纸面向里、大小分别为Ia=1A,Ib=2A,Ic=3A和Id=4A的恒定电流,已知离通电长导线相同距离的点,磁感应强度的大小与电流大小成正比,忽略电流间的相互作用,若电流Ia在正方形的几何中心O点处产生的磁感应强度大小为1T,则O点处实际的磁感应强度的大小及方向分别为( )
如图所示,现有四条完全相同的垂直于纸面放置的长直导线,横截面分别位于一正方形abcd的四个顶点上,直导线分别通有方向垂直纸面向里、大小分别为Ia=1A,Ib=2A,Ic=3A和Id=4A的恒定电流,已知离通电长导线相同距离的点,磁感应强度的大小与电流大小成正比,忽略电流间的相互作用,若电流Ia在正方形的几何中心O点处产生的磁感应强度大小为1T,则O点处实际的磁感应强度的大小及方向分别为( )| A. | 2$\sqrt{2}$T,由O点垂直指向ab方向 | B. | 2$\sqrt{2}$T,由O点垂直指向ad方向 | ||
| C. | 10T,垂直纸面向里 | D. | 10T,垂直纸面向外 |
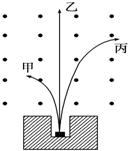 图是放射源放出的三种射线经过匀强磁场后分裂成三束,
图是放射源放出的三种射线经过匀强磁场后分裂成三束, 用均匀导线弯成正方形闭合线框abcd,线框每边长8.0cm,每边电阻为0.010Ω,把线框放在磁感强度为B=0.050T的匀强磁场中,并使它绕OO′以ω=100rad/s的匀角速度旋转,旋转方向如图所示.已知轴OO′在线框平面内,并且垂直于B,Od=3Oa,Oc=3Ob.当线框平面转至与B平行的瞬时(如图示位置).
用均匀导线弯成正方形闭合线框abcd,线框每边长8.0cm,每边电阻为0.010Ω,把线框放在磁感强度为B=0.050T的匀强磁场中,并使它绕OO′以ω=100rad/s的匀角速度旋转,旋转方向如图所示.已知轴OO′在线框平面内,并且垂直于B,Od=3Oa,Oc=3Ob.当线框平面转至与B平行的瞬时(如图示位置). 如图所示,一倾斜放置的传送带与水平面的倾角θ=37°,在电动机的带动下以v=2m/s的速率顺时针方向匀速运行,M、N为传送带的两个端点,MN两点间的距离L=7m,N端有一离传送带很近的挡板P可将传送带上的物块挡住,在传送带上的O处由静止释放一质量为1kg的可视为质点的木块,木块与传送带间的动摩擦因数μ=0.5.木块由静止释放后沿传送带向下运动,并与挡板P发生碰撞,已知碰撞时间极短,木块B与挡板P碰撞前后速度大小不变,OM间距离L=3m,sin37°=0.6,cos37°=0.8,g取10m/s2,传送带与轮子间无相对滑动,不计轮轴处的摩擦.
如图所示,一倾斜放置的传送带与水平面的倾角θ=37°,在电动机的带动下以v=2m/s的速率顺时针方向匀速运行,M、N为传送带的两个端点,MN两点间的距离L=7m,N端有一离传送带很近的挡板P可将传送带上的物块挡住,在传送带上的O处由静止释放一质量为1kg的可视为质点的木块,木块与传送带间的动摩擦因数μ=0.5.木块由静止释放后沿传送带向下运动,并与挡板P发生碰撞,已知碰撞时间极短,木块B与挡板P碰撞前后速度大小不变,OM间距离L=3m,sin37°=0.6,cos37°=0.8,g取10m/s2,传送带与轮子间无相对滑动,不计轮轴处的摩擦. 如图所示,质量为m=60kg的滑雪运动员(可视作质点),在平台上滑行一段距离后水平滑出,从空中运动一段时间后,从A点恰好沿圆弧切线的方向进入半径为R=8.0m的竖直圆弧轨道中.然后在摩擦阻力的作用下沿竖直圆弧轨道作匀速圆周运动.已知A、B为圆弧两端点,其连线水平,对应圆心角为θ=120°,平台与AB连线的高度差为h=2.4m.(忽略空气阻力g=10m/s2)求:
如图所示,质量为m=60kg的滑雪运动员(可视作质点),在平台上滑行一段距离后水平滑出,从空中运动一段时间后,从A点恰好沿圆弧切线的方向进入半径为R=8.0m的竖直圆弧轨道中.然后在摩擦阻力的作用下沿竖直圆弧轨道作匀速圆周运动.已知A、B为圆弧两端点,其连线水平,对应圆心角为θ=120°,平台与AB连线的高度差为h=2.4m.(忽略空气阻力g=10m/s2)求: 在研究微型电动机的性能时,应用如图所示的实验电路,调节滑动变阻器R并控制电动机停止转动时,电流表和电压表的示数分别为0.50A和1.0V.重新调节R并使电动机恢复正常运转,此时电流表和电压表的示数分别为2.0A和25.0V.则这台电动机正常运转时输出功率为( )
在研究微型电动机的性能时,应用如图所示的实验电路,调节滑动变阻器R并控制电动机停止转动时,电流表和电压表的示数分别为0.50A和1.0V.重新调节R并使电动机恢复正常运转,此时电流表和电压表的示数分别为2.0A和25.0V.则这台电动机正常运转时输出功率为( )